题目内容
在△ABC中,三内角A,B,C所对的边分别为a,b,c,且b2=a2-ac+c2,C-A=90°,则cosAcosC= .
考点:余弦定理
专题:计算题,解三角形
分析:根据余弦定理b2=a2+c2-2accosB的式子,结合题中等式解出B=
,从而得到cos(A+C)=-cosB=-
,又因为C-A=90°得cos(A-C)=0,利用两角和与差的余弦公式联解,即可得到cosAcosC的值.
| π |
| 3 |
| 1 |
| 2 |
解答:
解:∵在△ABC中,b2=a2-ac+c2,
∴由b2=a2+c2-2accosB,得cosB=
,
结合B∈(0,π)得B=
,
由此可得cos(A+C)=cosAcosC-sinAsinC=-cosB=-
,
又∵C-A=90°,可得cos(A-C)=cosAcosC+sinAsinC=cos(-90°)=0,
∴两式相加,得2cosAcosC=-
,解之得cosAcosC=-
.
故答案为:-
.
∴由b2=a2+c2-2accosB,得cosB=
| 1 |
| 2 |
结合B∈(0,π)得B=
| π |
| 3 |
由此可得cos(A+C)=cosAcosC-sinAsinC=-cosB=-
| 1 |
| 2 |
又∵C-A=90°,可得cos(A-C)=cosAcosC+sinAsinC=cos(-90°)=0,
∴两式相加,得2cosAcosC=-
| 1 |
| 2 |
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题给出三角形边的平方关系和C-A的值,求cosAcosC之值.着重考查了两角和与差的余弦公式、利用正余弦定理解三角形等知识,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
集合M={x|x>0},集合N={x|1-x>0},则M∩N等于( )
| A、(0,1) |
| B、(-∞,0) |
| C、(-∞,-1) |
| D、(-∞,1) |
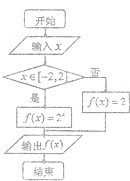 阅读如图所示的程序框图,如果输出的函数值在区间[
阅读如图所示的程序框图,如果输出的函数值在区间[| 1 |
| 4 |
| 1 |
| 2 |
| A、(-∞,-2) |
| B、[-2,-1] |
| C、[-1,2] |
| D、(2,+∞) |
某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.为调查产品的销售情况,现进行两种调查:①从这600个销售点中抽取一个容量为100的样本;②在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,则完成①、②这两项调查宜采用的抽样方法依次是( )
| A、分层抽样法,系统抽样法 |
| B、分层抽样法,简单随机抽样法 |
| C、系统抽样法,分层抽样法 |
| D、简单随机抽样法,分层抽样法 |
在△ABC中,∠A、∠B、∠C的对边分别为a、b、c,已知bcosB=acosA,则△ABC的形状是( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰三角形或直角三角形 |
函数f(x)=
的图象大致为( )
|
A、 |
B、 |
C、 |
D、 |
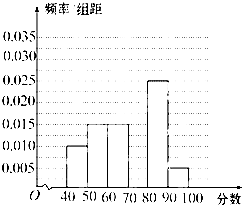 2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
2012年3月10日某校组织同学听取了温家宝总理所作的政府工作报告,并进行了检测,从参加检测的高二学生中随机抽出60名学生,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.观察图形的信息,回答下列问题: 已知函数f(x)=2sinxcos(x-φ)-
已知函数f(x)=2sinxcos(x-φ)-