题目内容

3．设随机变量X服从二项分布，且期望E（X）=3，P=$\frac{1}{5}$，则方差D（X）等于（　　）
A．$\frac{3}{5}$B．$\frac{4}{5}$C．$\frac{12}{5}$D．2

分析 由二项分布性质求出n=15，由此能求出方差D（X）．

解答 解：∵随机变量X服从二项分布，且期望E（X）=3，P=$\frac{1}{5}$，
∴n×$\frac{1}{5}$=3，解得n=15，
∴方差D（X）=np（1-p）=15×$\frac{1}{5}×\frac{4}{5}$=$\frac{12}{5}$．
故选：C．

点评 本题考查离散型随机变量的方差的求法，是基础题，解题时要认真审题，注意二项分布的性质的合理运用．

练习册系列答案
相关题目
13．在△ABC中，角A，B，C所对应的边分别为a，b，c，已知B=$\frac{π}{4}$，cosA-cos2A=0
（1）求角C；  
（2）若b2+c2=a-bc+2，求a，c值．
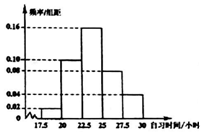14．某校调查了200名学生每周的自习时间（单位：小时），制成了如图所示的频率分布直方图，其中自习时间的范围是[17.5，30]，样本数据分组为[17.5，20），[17.5，20），[20，22.5），[22.5，25），[25，27.5），[27.5，30]．根据直方图，这200名学生中每周的自习时间不少于24小时的人数是（　　）
A．76B．92C．108D．114
11．现有四个点P1（0，-1），P2（-1，-1），P3（-1，$\frac{\sqrt{3}}{2}$），P4（-1，-$\frac{\sqrt{3}}{2}$），其中只有三个点在椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）是否存在过点M（1，0）的直线l，使得直线l与椭圆C交于A，B两点，线段AB的垂直平分线与x轴交于点N，且满足AB=2$\sqrt{10}$|MN|，若存在，求出直线l的方程，若不存在，请说明理由．
18．在如图所示的茎叶图中，甲、乙两组数据的中位数的和是64．
8．估算1.046精确到0.01的近似值为（　　）
A．1.26B．1.27C．1.36D．1.37
15．若集合P={x|0≤x≤3}，Q={x|x＞1}，则P∩Q=（　　）
A．{x|x≥0}B．{x|x＞1}C．{x|1＜x≤3}D．{x|1≤x≤3}
12．已知函数f（x）=ax2+ax+2．
（1）对任意的x∈R．f（x）＞0恒成立，求a的取值范围；
（2）若对于a∈[-1，1]，f（x）＜-a+5恒成立，求x的取值范围．
2．某几何体的三视图如图所示，则该几何体的体积是（　　）
A．3B．4C．5D．6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网