题目内容
6.因为i是虚数单位,复数$z=\frac{{{i^{2017}}}}{1+i}$,则z的共轭复数是( )| A. | $\frac{1}{2}+\frac{i}{2}$ | B. | $\frac{1}{2}-\frac{i}{2}$ | C. | $-\frac{1}{2}+\frac{i}{2}$ | D. | $-\frac{1}{2}-\frac{i}{2}$ |
分析 利用复数的周期性、共轭复数的定义即可得出.
解答 解:i2017=(i4)504•i=i,
复数$z=\frac{{{i^{2017}}}}{1+i}$=$\frac{i}{1+i}$=$\frac{i(1-i)}{(1+i)(1-i)}$=$\frac{1}{2}$+$\frac{1}{2}$i,则z的共轭复数$\overline{z}$=$\frac{1}{2}$-$\frac{1}{2}$i,
故选:B.
点评 本题考查了复数的运算法则、复数的周期性、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
1.已知复数$z=\frac{5-i}{1-i}$,则z的虚部为( )
| A. | 2i | B. | 3i | C. | 2 | D. | 3 |
11.已知集合A={x||x-1|<2},B={x|-1<x<m+1},若x∈A成立的一个必要不充分条件是x∈B,则实数m的取值范围是( )
| A. | [2,+∞) | B. | (-∞,2] | C. | (2,+∞) | D. | (-∞,2) |
18.已知全集U={1,2,3,4,5,6},集合A={1,2,4},B={2,4,6},则A∩(∁UB)=( )
| A. | {1} | B. | {2} | C. | {4} | D. | {1,2} |
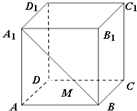 如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②
如图,棱长为1的正方体ABCD-A1B1C1D1中,M为线段A1B上的动点,则下列结论正确的有①②