题目内容
14．集合{1，2，3，4}的不含有2的真子集为∅，{1}，{3}，{4}，{1，3}，{1，4}，{3，4}，{1，3，4}．分析 去掉2，分别由集合中没有元素，1个元素，2个元素，3个元素求出即可．
解答 解：集合{1，2，3，4}的不含有2的真子集为：
∅，{1}，{3}，{4}，{1，3}，{1，4}，{3，4}，{1，3，4}，
故答案为：∅，{1}，{3}，{4}，{1，3}，{1，4}，{3，4}，{1，3，4}．
点评 本题考查了集合的真子集问题，是一道基础题．
练习册系列答案
优等生题库系列答案
相关题目
2．如图，∠ACB=90°，CD⊥AB于D，AD=3，CD=2，则$\frac{AC}{BC}$的值为（ ）
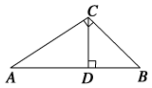
| A． | $\frac{3}{2}$ | B． | $\frac{9}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{4}{9}$ |
19．若集合A∪B=B∩C，则集合A，B，C的关系下列表示正确的是（ ）
| A． | A⊆B⊆C | B． | C⊆B⊆A | C． | B⊆C⊆A | D． | B⊆A⊆C |
6．因为i是虚数单位，复数$z=\frac{{{i^{2017}}}}{1+i}$，则z的共轭复数是（ ）
| A． | $\frac{1}{2}+\frac{i}{2}$ | B． | $\frac{1}{2}-\frac{i}{2}$ | C． | $-\frac{1}{2}+\frac{i}{2}$ | D． | $-\frac{1}{2}-\frac{i}{2}$ |