题目内容
5名运动员争夺3项比赛冠军(每项比赛无并列冠军),获得冠军的可能种数为( )
| A、35 | ||
B、
| ||
C、
| ||
| D、53 |
考点:计数原理的应用
专题:排列组合
分析:每个冠军的情况都有5种,共计3个冠军,故分3步完成,根据分步计数原理,运算求得结果.
解答:
解:每一项冠军的情况都有5种,故5名学生争夺三项冠军,获得冠军的可能的种数是 53,
故选:D.
故选:D.
点评:本题主要考查分步计数原理的应用,属于基础题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
已知双曲线的渐近线方程为y=±x,且过点(-
,-3),则双曲线的方程为( )
| 2 |
A、
| ||
| B、x2-y2=7 | ||
| C、y2-x2=7 | ||
D、-
|
函数f(x)=-x3+x2+tx+t在(-1,1)上是增函数,则t的取值范围是( )
| A、t>5 | B、t<5 |
| C、t≥5 | D、t≤5 |
在回归分析中,相关指数R2的值越小,说明残差平方和( )
| A、越小 | B、越大 |
| C、可能大也可能小 | D、以上都不对 |
椭圆34x2+9y2=306的焦点坐标是( )
| A、(-5,0)、(5,0) |
| B、(-4,0)、(4,0) |
| C、(0,-5)、(0,5) |
| D、(0,-4)、(0,4) |
已知直线
,的倾斜角的度数为( )
|
| A、30 | B、60 |
| C、120 | D、150 |
若△ABC的内角满足sinA+
sinB=2sinC,则cosC的最小值是( )
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
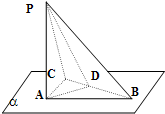 如图,BC是Rt△ABC的斜边,过A作△ABC所在平面α垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数
如图,BC是Rt△ABC的斜边,过A作△ABC所在平面α垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数