题目内容
若函数f(x)=x3+ax2-2x+5在区间(
,
)上不是单调函数,则实数a的取值范围是 .
| 1 |
| 3 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的导数,由题意得函数的导数在区间(
,
)上至少有一个零点,分两种情况①若只有一个零点;②若有两个不同零点,进行讨论,综合可得实数a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
解答:
解:∵f(x)=x3+ax2-2x+5
∴f′(x)=3x2+2ax-2
根据题意,函数在区间(
,
)上至少有一个零点
①若只有一个零点,f′(
)f′(
)<0,得a∈(
,
),
②若有两个不同零点,则
,解得:a∈∅,
综上:a∈(
,
),
故答案为:(
,
).
∴f′(x)=3x2+2ax-2
根据题意,函数在区间(
| 1 |
| 3 |
| 1 |
| 2 |
①若只有一个零点,f′(
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
②若有两个不同零点,则
|
综上:a∈(
| 5 |
| 4 |
| 5 |
| 2 |
故答案为:(
| 5 |
| 4 |
| 5 |
| 2 |
点评:本题考查了利用导数研究三次多项式函数的单调性,从而求参数a的取值范围,属于中档题.解题时应该注意导数零点个数的讨论,以免出现只一个零点的误解.

练习册系列答案
相关题目
在回归分析中,相关指数R2的值越小,说明残差平方和( )
| A、越小 | B、越大 |
| C、可能大也可能小 | D、以上都不对 |
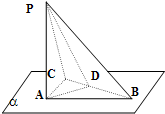 如图,BC是Rt△ABC的斜边,过A作△ABC所在平面α垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数
如图,BC是Rt△ABC的斜边,过A作△ABC所在平面α垂线AP,连PB、PC,过A作AD⊥BC于D,连PD,那么图中直角三角形的个数