题目内容
已知sinα=
，且α是第一象限角，求cosα，tanα．
| 1 |
| 2 |
考点：同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：依题意，可求得cosα，继而可得tanα．
解答：
解：∵sinα=
，且α是第一象限角，
∴cosα=
=
=
，tanα=
=
=
．
| 1 |
| 2 |
∴cosα=
| 1-sin2α |
1-
|
| ||
| 2 |
| sinα |
| cosα |
| ||||
|
| ||
| 3 |
点评：本题考查同角三角函数基本关系的运用，属于基本知识的考查．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
相关题目
若全集U=Z，集合A={n|
∈z}，集合B={n|
∈z}，则A∩{CuB}是（ ）
| n |
| 2 |
| n |
| 3 |
| A、{n|n=3k+1，k∈z} |
| B、{n|n=4k或n=4k+2，k∈z} |
| C、{n|n=6k±1，k∈z} |
| D、{n|n=6k±2，k∈z} |
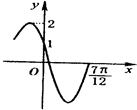
如图是函数f（x）=Asin（ωx+φ）（A＞0，0＜ω＜3，0＜φ＜π）的图象的一部分，则ωφ=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|