题目内容
5.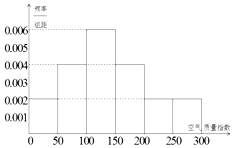 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):
某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过300):| 空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅰ)请估算2017年(以365天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校2017年6月7、8、9日将作为高考考场,若这三天中某天出现5级重度污染,需要净化空气费用10000元,出现6级严重污染,需要净化空气费用20000元,记这三天净化空气总费用为X元,求X的分布列及数学期望.
分析 (I)利用直方图的性质即可得出.
(Ⅱ)由题可知,X的所有可能取值为:0,10000,20000,30000,40000,50000,60000,利用二项分布列的概率与数学期望计算公式即可得出.
解答 解:(Ⅰ)由直方图可估算2017年(以365天计算)全年空气质量优良的天数为:
(0.1+0.2)×365=0.3×365=109.5≈110(天).------------(4分)
(Ⅱ)由题可知,X的所有可能取值为:0,10000,20000,30000,40000,50000,60000,------------(6分)
则:$P(X=0)={(\frac{4}{5})^3}=\frac{64}{125}$,$P(X=10000)=C_3^1×\frac{1}{10}×{(\frac{4}{5})^2}=\frac{24}{125}$,$P(X=20000)=C_3^2×{(\frac{1}{10})^2}×(\frac{4}{5})+C_3^1×(\frac{1}{10})×{(\frac{4}{5})^2}=\frac{108}{500}=\frac{27}{125}$,$P(X=30000)={(\frac{1}{10})^3}+C_3^1×\frac{1}{10}×C_2^1×\frac{1}{10}×\frac{4}{5}=\frac{49}{1000}$,$P(X=40000)=C_3^2×{(\frac{1}{10})^2}×\frac{1}{10}+C_3^2×{(\frac{1}{10})^2}×\frac{4}{5}=\frac{27}{1000}$,$P(X=50000)=C_3^2×{(\frac{1}{10})^2}×\frac{1}{10}=\frac{3}{1000}$,$P(X=60000)={(\frac{1}{10})^3}=\frac{1}{1000}$.
∴X的分布列为
| X | 0 | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 |
| P | $\frac{64}{125}$ | $\frac{24}{125}$ | $\frac{27}{125}$ | $\frac{49}{1000}$ | $\frac{27}{1000}$ | $\frac{3}{1000}$ | $\frac{1}{1000}$ |
点评 本题考查了频率分布直方图的性质、二项分布列的概率与数学期望计算公式,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{\sqrt{3}+i}{2}$ | B. | -$\sqrt{3}$-i | C. | -$\sqrt{3}$+i | D. | -$\frac{\sqrt{3}+i}{2}$ |
| A. | {3,4} | B. | {1,2,3} | C. | {1,2} | D. | {1,2,3,4} |
 如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )
如图所示,在正方体ABCD-A1B1C1D1中,已知M,N分别是BD和AD的中点,则B1M与D1N所成角的余弦值为( )| A. | $\frac{{\sqrt{30}}}{10}$ | B. | $\frac{{\sqrt{30}}}{15}$ | C. | $\frac{{\sqrt{30}}}{30}$ | D. | $\frac{{\sqrt{15}}}{15}$ |