题目内容
【题目】已知椭圆![]() 与直线
与直线![]() 有且只有一个交点,点P为椭圆C上任一点,
有且只有一个交点,点P为椭圆C上任一点,![]() ,
,![]() .若
.若![]() 的最小值为
的最小值为![]() .
.
(1)求椭圆C的标准方程;
(2)设直线![]() 与椭圆C交于不同两点A,B,点O为坐标原点,且
与椭圆C交于不同两点A,B,点O为坐标原点,且![]() ,当
,当![]() 的面积S最大时,求
的面积S最大时,求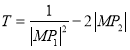 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)设点![]() ,利用向量的坐标运算研究
,利用向量的坐标运算研究![]() 的最小值,建立方程,求出
的最小值,建立方程,求出![]() 的值,即可得椭圆C的标准方程;
的值,即可得椭圆C的标准方程;
(2)设![]() ,
,![]() ,
,![]() ,将直线
,将直线![]() 与椭圆C联立,可得
与椭圆C联立,可得![]() 和
和![]() ,求出点O到直线l的距离,即可求出
,求出点O到直线l的距离,即可求出![]() 的面积S的表达式,利用基本不等式,求面积S的最大值,根据最大值的成立条件和前面求出的
的面积S的表达式,利用基本不等式,求面积S的最大值,根据最大值的成立条件和前面求出的![]() 和
和![]() ,可得点M的轨迹方程,进而可得
,可得点M的轨迹方程,进而可得![]() 的范围,将
的范围,将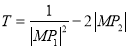 转化为
转化为![]() ,利用导数研究单调性即可求出
,利用导数研究单调性即可求出![]() 的取值范围.
的取值范围.
解:(1)设点![]() ,由题意知
,由题意知![]() ,
,![]() ,则
,则
![]() ,
,
当![]() 时,
时,![]() 取得最小值,即
取得最小值,即![]() ,
,
![]() ,
,![]() 故椭圆C的标准方程为
故椭圆C的标准方程为![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,则
,则
由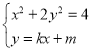 得
得![]() ,
,
![]() ,
,![]() ,
,
点O到直线l的距离![]() ,
,
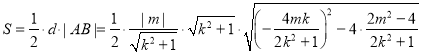
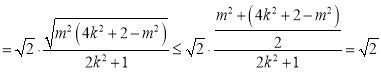 ,
,
S取得最大值![]() ,当且仅当
,当且仅当![]() 即
即![]() ,①
,①
此时![]() ,
,![]() ,
,
即![]() ,
,![]() 代入①式整理得,
代入①式整理得,![]() ,
,
即点M的轨迹为椭圆![]() ,
,
且点![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,即
的左、右焦点,即![]() ,
,
记![]() ,则
,则![]() ,
,
从而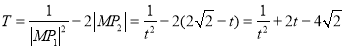 ,则
,则![]() ,
,
令![]() 可得
可得![]() ,即在T在
,即在T在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
且![]() ,
,![]() ,
,
故T的取值范围为![]() .
.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目