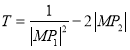题目内容
【题目】已知实数![]() ,设函数
,设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若对任意的
时,若对任意的![]() ,均有
,均有![]() ,求
,求![]() 的取值范围.
的取值范围.
注:![]() 为自然对数的底数.
为自然对数的底数.
【答案】(1)![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增;(2)
内单调递增;(2)![]()
【解析】
(1)求导后取出极值点,再分![]() ,
,![]() 两种情况进行讨论即可.
两种情况进行讨论即可.
(2)当![]() 时得出
时得出![]() 的一个取值范围,再讨论
的一个取值范围,再讨论![]() 时的情况,再对
时的情况,再对![]() 时构造函数两边取对数进行分析论证
时构造函数两边取对数进行分析论证![]() 时
时![]() 恒成立.
恒成立.
(1)由![]() ,解得
,解得![]() .
.
①若![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减.
内单调递减.
②若![]() ,则当
,则当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递增;
内单调递增;
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 内单调递减.
内单调递减.
综上所述,![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增.
内单调递增.
(2)![]() ,即
,即![]() .
.
令![]() ,得
,得![]() ,则
,则![]() .
.
当![]() 时,不等式
时,不等式![]() 显然成立,
显然成立,
当![]() 时,两边取对数,即
时,两边取对数,即![]() 恒成立.
恒成立.
令函数![]() ,即
,即![]() 在
在![]() 内恒成立.
内恒成立.
由![]() ,得
,得![]() .
.
故当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
因此![]() .
.
令函数![]() ,其中
,其中![]() ,
,
则![]() ,得
,得![]() ,
,
故当![]() 时,
时,![]() ,
,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() 单调递增.
单调递增.
又![]() ,
,![]() ,
,
故当![]() 时,
时,![]() 恒成立,因此
恒成立,因此![]() 恒成立,
恒成立,
即当![]() 时,对任意的
时,对任意的![]() ,均有
,均有![]() 成立.
成立.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案【题目】“绿水青山就是金山银山”的生态文明发展理念已经深入人心,这将推动新能源汽车产业的迅速发展.下表是近几年我国某地区新能源乘用车的年销售量与年份的统计表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
销量(万台) | 8 | 10 | 13 | 25 | 24 |
某机构调查了该地区30位购车车主的性别与购车种类情况,得到的部分数据如下表所示:
购置传统燃油车 | 购置新能源车 | 总计 | |
男性车主 | 6 | 24 | |
女性车主 | 2 | ||
总计 | 30 |
(1)求新能源乘用车的销量![]() 关于年份
关于年份![]() 的线性相关系数
的线性相关系数![]() ,并判断
,并判断![]() 与
与![]() 是否线性相关;
是否线性相关;
(2)请将上述![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为购车车主是否购置新能源乘用车与性别有关;
的把握认为购车车主是否购置新能源乘用车与性别有关;
(3)若以这30名购车车主中购置新能源乘用车的车主性别比例作为该地区购置新能源乘用车的车主性别比例,从该地区购置新能源乘用车的车主中随机选取50人,记选到女性车主的人数为X,求X的数学期望与方差.
参考公式: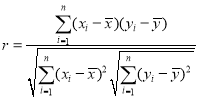 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,则可判断
,则可判断![]() 与
与![]() 线性相关.
线性相关.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |