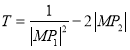Question

【题目】已知A是圆锥的顶点，是圆锥底面的直径，C是底面圆周上一点，，与底面所成角的大小为60°，过点A作截面，截去部分后的几何体如图所示.

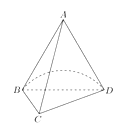
（1）求异面直线与所成角的大小；

（2）求该几何体的体积.

Answer 1

【答案】（1）；（2）

【解析】

（1）设BD的中点为O，连接CO，并延长交弧BD于E，连接EA，ED，

则ED∥BC，则∠ADE是异面直线BC与AD所成的角，在△AED中，结合已知量与余弦定理求出∠ADE．（2）该几何体的体积V（S△BCD+S半圆）AO，由此能求出结果．

（1）设BD的中点为O，连接CO，并延长交弧BD于E，连接EA，ED，

则ED∥BC，则∠ADE是异面直线BC与AD所成的角，

连结OA，

∵A是圆锥的顶点，BD是圆锥底面的直径，,

∵BD＝2，∴CO＝EO＝1，

且OA⊥平面BCD．

∵与底面所成角的大小为60°，

∴AC与底面所成角的大小为，即，

∴AC＝AD2，又CO＝BO＝1，∴BC＝DE＝1,

在△AED中，cos∠ADE．

∴异面直线PC与SB所成的角为arccos.

（2）该几何体为三棱锥与半个圆锥的组合体，

∵AO，∠BCD＝90°，∴CD，

该几何体的体积V（S△BCD+S半圆）AO

．