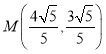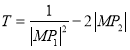题目内容
【题目】在平面直角坐标系上,有一点列![]() ,设点
,设点![]() 的坐标
的坐标![]() (
(![]() ),其中
),其中![]() . 记
. 记![]() ,
,![]() ,且满足
,且满足![]() (
(![]() ).
).
(1)已知点![]() ,点
,点![]() 满足
满足![]() ,求
,求![]() 的坐标;
的坐标;
(2)已知点![]() ,
,![]() (
(![]() ),且
),且![]() (
(![]() )是递增数列,点
)是递增数列,点![]() 在直线
在直线![]() :
:![]() 上,求
上,求![]() ;
;
(3)若点![]() 的坐标为
的坐标为![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1) ![]() (2)
(2) ![]() (3)4066272
(3)4066272
【解析】
(1)由题意求出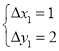 即可求得
即可求得![]() 点坐标.(2)由题意求得
点坐标.(2)由题意求得![]() ,又由
,又由![]() 是递增数列得到
是递增数列得到![]() ,由题中所给条件即可求得
,由题中所给条件即可求得![]() ,代入
,代入![]() 即可.(3)先求出
即可.(3)先求出![]() 整理,再由题意利用放缩法得到
整理,再由题意利用放缩法得到![]() ,对
,对![]() 取特殊值即可得到
取特殊值即可得到![]() .
.
(1)因为![]() 、
、![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]() , 所以
, 所以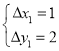 ,
,
所以![]() ,
,![]() ,
,
所以点![]() 的坐标为
的坐标为 ![]() .
.
(2)因为![]() ,
,![]() (
(![]()
得![]() ,
,
又![]() ,
,![]() ,得
,得![]() (
(![]() ),
),
因为![]() ,而
,而![]() (
(![]() )是递增数列,
)是递增数列,
故![]() (
(![]() ),
),
![]() ,
,
所以![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
得![]() .
.
(3)![]() ,
,
![]() ,
,
记![]()
![]()
![]() ,
,
因为![]() 是偶数,
是偶数,![]() ,
,
![]() ,
,
当![]() ,
,
![]() 时(取法不唯一),
时(取法不唯一),![]() ,
,
所以![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目