题目内容
已知函数f(x)=2cosx(sinx+cosx),x∈R.
(1)求f(x)的最小正周期T;
(2)求f(x)的最大值,并求f(x)取最大值时自变量x的集合.
(1)求f(x)的最小正周期T;
(2)求f(x)的最大值,并求f(x)取最大值时自变量x的集合.
(1)f(x)=2cosx(sinx+cosx)=sin2x+cos2x+1=
sin(2x+
)+1,
∵ω=2,∴T=
=π;
(2)由(1)知f(x)的最大值M=
+1,
当f(x)=
+1时,sin(2x+
)=1,
∴2x+
=2kπ+
,
即x=kπ+
,k∈Z,
则所求自变量x的集合为{x|x=kπ+
,k∈Z}.
| 2 |
| π |
| 4 |
∵ω=2,∴T=
| 2π |
| 2 |
(2)由(1)知f(x)的最大值M=
| 2 |
当f(x)=
| 2 |
| π |
| 4 |
∴2x+
| π |
| 4 |
| π |
| 2 |
即x=kπ+
| π |
| 8 |
则所求自变量x的集合为{x|x=kπ+
| π |
| 8 |

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
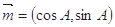 ,
, ,若
,若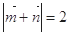
 的面积.
的面积. 中,
中, 所对的边分别为
所对的边分别为 ,且
,且 ,
, .
. 的值;
的值; 的值.
的值.
 ,
, ,
, .求
.求 的值.
的值.