题目内容
已知α、β∈(0,
),且sinα=
,cosβ=
,
(1)求cos(α-β)
(2)求α-β
| π |
| 2 |
| ||
| 5 |
| ||
| 10 |
(1)求cos(α-β)
(2)求α-β
(1)∵sinα=
,cosβ=
,α、β∈(0,
),
∴cosα=
=
sinβ=
2=
∴cos(α-β)=cosαcosβ+sinαsinβ=
×
+
×
=
(2)∵α,β∈(0,
),
∴-β∈(-
,0)
∴α-β∈(-
,
)
∵cos(α-β)=
∴α-β=
或-
| ||
| 5 |
| ||
| 10 |
| π |
| 2 |
∴cosα=
1-(
|
2
| ||
| 5 |
1-(
|
3
| ||
| 10 |
∴cos(α-β)=cosαcosβ+sinαsinβ=
2
| ||
| 5 |
| ||
| 10 |
| ||
| 5 |
3
| ||
| 10 |
| ||
| 2 |
(2)∵α,β∈(0,
| π |
| 2 |
∴-β∈(-
| π |
| 2 |
∴α-β∈(-
| π |
| 2 |
| π |
| 2 |
∵cos(α-β)=
| ||
| 2 |
∴α-β=
| π |
| 4 |
| π |
| 4 |

练习册系列答案
相关题目
 ,且
,且 ,
, ,
, .
. 的值;(2)求ΔABC的面积.
的值;(2)求ΔABC的面积. ,函数
,函数 的最小正周期为
的最小正周期为 : (Ⅰ) 求
: (Ⅰ) 求 的单调增区间 (Ⅱ) 在
的单调增区间 (Ⅱ) 在 中,
中, 分别是角A、B、C的对边,若
分别是角A、B、C的对边,若 ,
, ,
,  ,求
,求 的值
的值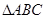 中,角
中,角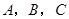 所对的边分别为
所对的边分别为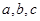 ,角
,角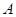 为锐角,且
为锐角,且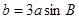 ,则
,则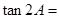 .
.