题目内容
已知数列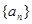 的前
的前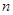 项和为
项和为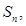
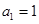 ,对于任意的
,对于任意的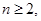 恒有
恒有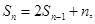
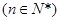
(1) 求数列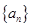 的通项公式
的通项公式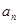
(2)若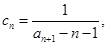 证明:
证明:
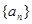 的前
的前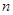 项和为
项和为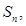
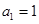 ,对于任意的
,对于任意的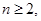 恒有
恒有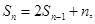
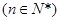
(1) 求数列
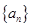 的通项公式
的通项公式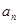
(2)若
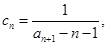 证明:
证明:
(1)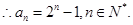 (2)关键是得到
(2)关键是得到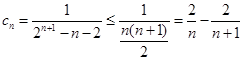
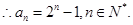 (2)关键是得到
(2)关键是得到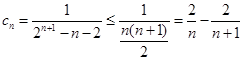
试题分析:解: (1) 当
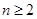 时,
时,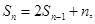 又
又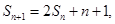 两式相减得:
两式相减得: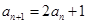

又
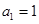 ,
,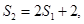 得
得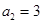 ,满足
,满足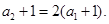
 数列
数列 是以
是以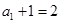 为首项,2为公比的等比数列.
为首项,2为公比的等比数列. 得
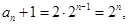
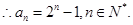
(2)证明:由(1)可知
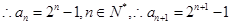
由
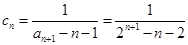
因为
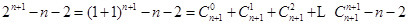
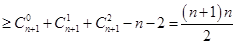
故
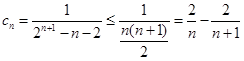 ,由
,由
当
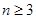 时,
时, 则不等式成立.
则不等式成立.另解:
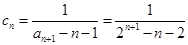
 ,当
,当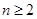 时,总有
时,总有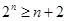 (用数学归纳法证明,略)
(用数学归纳法证明,略)当
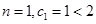
则
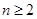 时,
时,
故
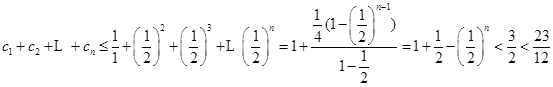
则不等式成立.
点评:求一般数列的问题时,常用的方法是裂变法和错位相减法,本题就用到裂变法。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
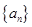 的首项
的首项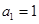 ,前
,前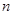 项和
项和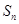 满足
满足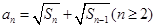 .
.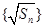 为等差数列,并求数列
为等差数列,并求数列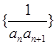 的前
的前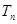 ,若对任意的
,若对任意的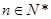 ,不等式
,不等式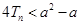 恒成立,求实数
恒成立,求实数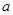 的取值范围.
的取值范围.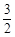 的等比数列
的等比数列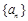 的前n项和为
的前n项和为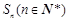 , 且
, 且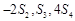 成等差数列.
成等差数列. 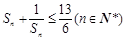 .
. 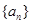 是公比大于
是公比大于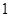 的等比数列,
的等比数列,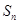 是
是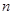 项和.若
项和.若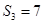 ,且
,且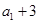 ,
,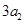 ,
,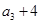 构成等差数列.
构成等差数列.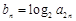 ,求数列
,求数列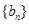 的前
的前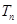 .
.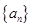 中,若
中,若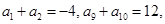 则
则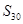 = .
= . 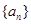 的前n项和为
的前n项和为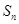 .已知
.已知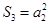 ,且
,且 成等比数列,求
成等比数列,求 中,
中,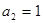 ,
,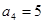 ,则
,则 =
=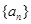 中,
中, 
 则
则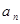 = .
= .