题目内容
等差数列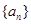 的前n项和为
的前n项和为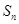 .已知
.已知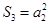 ,且
,且 成等比数列,求
成等比数列,求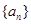 的通项公式.
的通项公式.
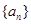 的前n项和为
的前n项和为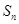 .已知
.已知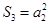 ,且
,且 成等比数列,求
成等比数列,求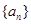 的通项公式.
的通项公式. 或
或
设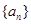 的公差为d.
的公差为d.
由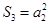 得
得 ,故
,故 或
或 .
.
由 成等比数列得
成等比数列得 .
.
又 ,
, ,
, ,
,
故 .
.
若 ,则
,则 ,所以
,所以 ,此时
,此时 ,不合题意;
,不合题意;
若 ,则
,则 ,解得
,解得 或
或 .
.
因此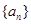 的通项公式为
的通项公式为 或
或 .
.
解答本题的关键是利用基本量思想和方程思想将题设两个条件结合在一起,得到数列的首项和等差.解答时需注意解方程时需注意公差d得零的情况的排除.
【考点定位】本题考查等差数列的通项公式、求和公式和等比中项等综合知识,考查学生的计算能力和转化分析能力.
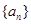 的公差为d.
的公差为d.由
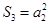 得
得 ,故
,故 或
或 .
.由
 成等比数列得
成等比数列得 .
.又
 ,
, ,
, ,
,故
 .
.若
 ,则
,则 ,所以
,所以 ,此时
,此时 ,不合题意;
,不合题意;若
 ,则
,则 ,解得
,解得 或
或 .
.因此
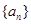 的通项公式为
的通项公式为 或
或 .
.解答本题的关键是利用基本量思想和方程思想将题设两个条件结合在一起,得到数列的首项和等差.解答时需注意解方程时需注意公差d得零的情况的排除.
【考点定位】本题考查等差数列的通项公式、求和公式和等比中项等综合知识,考查学生的计算能力和转化分析能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
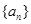 是公比为q的等比数列.
是公比为q的等比数列. 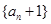 不是等比数列.
不是等比数列.  中,
中, ,则
,则 的值是 .
的值是 . 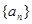 的前
的前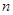 项和为
项和为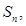
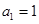 ,对于任意的
,对于任意的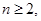 恒有
恒有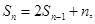
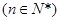
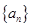 的通项公式
的通项公式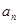
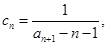 证明:
证明:
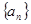 中,
中,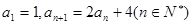 ,则通项公式
,则通项公式 =
=  为等差数列
为等差数列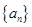 的前
的前 项和,
项和,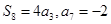 ,则
,则 =( )
=( )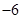


 是等差数列,
是等差数列, 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且
 的通项公式;
的通项公式; 为数列
为数列 的前
的前 项和,求
项和,求 .
.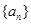 中,
中,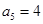 ,前9项和
,前9项和 ( )
( )