题目内容
已知正项数列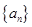 的首项
的首项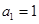 ,前
,前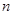 项和
项和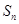 满足
满足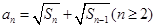 .
.
(Ⅰ)求证: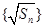 为等差数列,并求数列
为等差数列,并求数列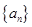 的通项公式;
的通项公式;
(Ⅱ)记数列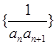 的前
的前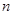 项和为
项和为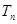 ,若对任意的
,若对任意的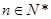 ,不等式
,不等式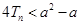 恒成立,求实数
恒成立,求实数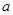 的取值范围.
的取值范围.
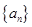 的首项
的首项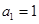 ,前
,前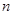 项和
项和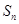 满足
满足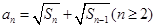 .
.(Ⅰ)求证:
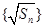 为等差数列,并求数列
为等差数列,并求数列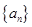 的通项公式;
的通项公式;(Ⅱ)记数列
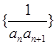 的前
的前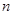 项和为
项和为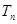 ,若对任意的
,若对任意的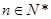 ,不等式
,不等式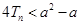 恒成立,求实数
恒成立,求实数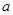 的取值范围.
的取值范围. (Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
 ;(Ⅱ)
;(Ⅱ) .
.试题分析:(Ⅰ)求证
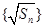 为等差数列,只需证
为等差数列,只需证 等于常数,由
等于常数,由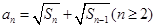 ,而
,而 ,代入整理可得
,代入整理可得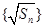 为等差数列,从而求出数列
为等差数列,从而求出数列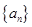 的通项公式
的通项公式 ;(Ⅱ)不等式
;(Ⅱ)不等式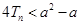 恒成立,转化为求
恒成立,转化为求 的最大值,而
的最大值,而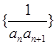 的前
的前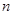 项和为
项和为 可用拆项相消法求得
可用拆项相消法求得 的最大值,从而解一元二次不等式得实数
的最大值,从而解一元二次不等式得实数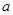 的取值范围.
的取值范围.试题解析:(Ⅰ)证明:当
 时,
时, ,又
,又 ,
, ,因为
,因为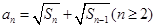 ,
, ,
, , 即
, 即 ,
, ,所以数列
,所以数列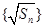 是首项为
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.由此可得
 ,由
,由 ,当
,当 时,
时,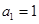 也适合,所以
也适合,所以 ;
;(Ⅱ)因为
 ,
,所以,
 ,
, ,对任意的
,对任意的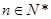 ,不等式
,不等式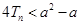 恒成立,
恒成立, ,解得
,解得 ,
,所以对任意的
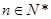 ,不等式
,不等式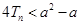 恒成立,实数
恒成立,实数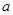 的取值范围
的取值范围 .
. 与
与 的关系,3、求数列的通项公式,4、数列求和,5、解一元二次不等式.
的关系,3、求数列的通项公式,4、数列求和,5、解一元二次不等式.
练习册系列答案
相关题目
 满足:
满足: 点
点 均在直线
均在直线 上.
上. 为等比数列,并求出数列
为等比数列,并求出数列 ,求数列
,求数列 的前
的前 项和
项和 .
. ,数列
,数列 前
前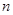 项和
项和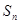 ,
,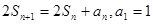 ,数列
,数列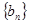 ,满足
,满足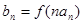 .(Ⅰ)求数列
.(Ⅰ)求数列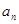 ;
;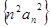 的前
的前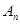 ,数列
,数列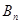 ,证明:
,证明: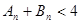 。
。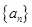 的公差
的公差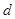 ≠0,
≠0,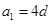 .若
.若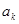 是
是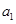 与
与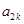 的等比中项,则
的等比中项,则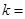 ( )
( ) ,则数列{an}的前n项和Sn的最小值为________.
,则数列{an}的前n项和Sn的最小值为________.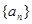 的前
的前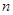 项和为
项和为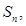
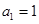 ,对于任意的
,对于任意的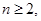 恒有
恒有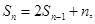
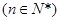
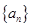 的通项公式
的通项公式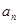
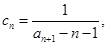 证明:
证明:
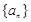 中,若
中,若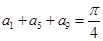 ,则
,则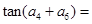 _________________.
_________________. 是等差数列,若
是等差数列,若 ,则数列
,则数列