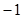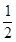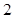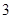题目内容
已知首项为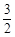 的等比数列
的等比数列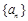 的前n项和为
的前n项和为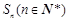 , 且
, 且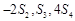 成等差数列.
成等差数列.
(Ⅰ) 求数列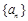 的通项公式;
的通项公式;
(Ⅱ) 证明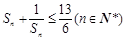 .
.
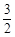 的等比数列
的等比数列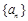 的前n项和为
的前n项和为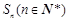 , 且
, 且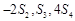 成等差数列.
成等差数列. (Ⅰ) 求数列
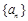 的通项公式;
的通项公式; (Ⅱ) 证明
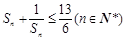 .
. (Ⅰ) 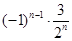 (Ⅱ)见解析
(Ⅱ)见解析
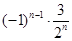 (Ⅱ)见解析
(Ⅱ)见解析(Ⅰ)设等比数列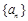 的公比为
的公比为 ,因为
,因为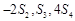 成等差数列,所以
成等差数列,所以
S4 + 2S2 =4S4 – S3,即 ,于是
,于是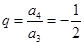 ,又
,又 =
=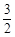 ,
,
所以等比数列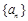 的通项公式为
的通项公式为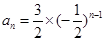 =
=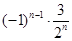 .
.
(Ⅱ)由(Ⅰ)得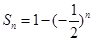 ,所以
,所以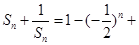
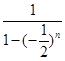 =
=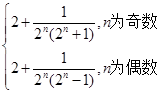 ,
,
当n为奇数时,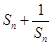 随n的增大而减小,所以
随n的增大而减小,所以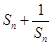
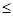
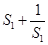 =
=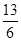 ;
;
当n为偶数时,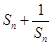 随n的增大而增大,所以
随n的增大而增大,所以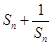
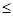
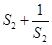 =
=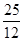 ,
,
故对于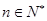 ,有
,有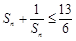 .
.
本题第(Ⅰ)问,由S3 + a3, S5 + a5, S4 + a4成等差数列可以求出公比,进而由等比数列的通项公式求出结果;第(Ⅱ)问,先求出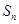 ,然后分n为奇数与偶数讨论得出数列
,然后分n为奇数与偶数讨论得出数列 的最大项与最小项的值.对第(Ⅰ)问,要注意细心计算;第二问,注意分n为奇数与偶数两种情况讨论.
的最大项与最小项的值.对第(Ⅰ)问,要注意细心计算;第二问,注意分n为奇数与偶数两种情况讨论.
【考点定位】本小题主要考查等差数列的概念,等比数列的概念、通项公式、前n项和公式,数列的基本性质等基础知识,考查分类讨论的思想,考查运算能力、分析问题和解决问题的能力.
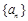 的公比为
的公比为 ,因为
,因为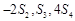 成等差数列,所以
成等差数列,所以S4 + 2S2 =4S4 – S3,即
 ,于是
,于是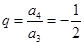 ,又
,又 =
=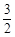 ,
,所以等比数列
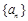 的通项公式为
的通项公式为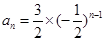 =
=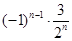 .
.(Ⅱ)由(Ⅰ)得
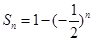 ,所以
,所以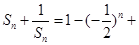
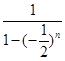 =
=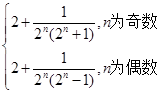 ,
,当n为奇数时,
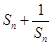 随n的增大而减小,所以
随n的增大而减小,所以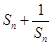
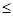
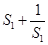 =
=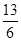 ;
;当n为偶数时,
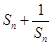 随n的增大而增大,所以
随n的增大而增大,所以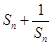
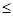
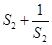 =
=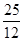 ,
,故对于
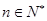 ,有
,有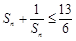 .
.本题第(Ⅰ)问,由S3 + a3, S5 + a5, S4 + a4成等差数列可以求出公比,进而由等比数列的通项公式求出结果;第(Ⅱ)问,先求出
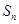 ,然后分n为奇数与偶数讨论得出数列
,然后分n为奇数与偶数讨论得出数列 的最大项与最小项的值.对第(Ⅰ)问,要注意细心计算;第二问,注意分n为奇数与偶数两种情况讨论.
的最大项与最小项的值.对第(Ⅰ)问,要注意细心计算;第二问,注意分n为奇数与偶数两种情况讨论.【考点定位】本小题主要考查等差数列的概念,等比数列的概念、通项公式、前n项和公式,数列的基本性质等基础知识,考查分类讨论的思想,考查运算能力、分析问题和解决问题的能力.

练习册系列答案
相关题目
 ,数列
,数列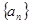 前
前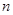 项和
项和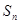 ,
,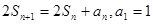 ,数列
,数列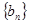 ,满足
,满足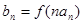 .(Ⅰ)求数列
.(Ⅰ)求数列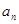 ;
;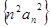 的前
的前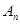 ,数列
,数列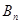 ,证明:
,证明: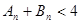 。
。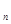 }为等差数列,S
}为等差数列,S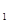 =
=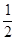 ,a
,a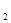 +a
+a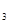 =3,则S
=3,则S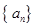 的前
的前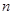 项和
项和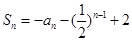 (
(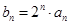 ,求证:数列
,求证:数列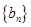 是等差数列,并求数列
是等差数列,并求数列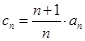 ,
,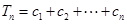 ,求使得
,求使得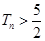 成立的最小正整数
成立的最小正整数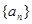 的前
的前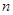 项和为
项和为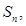
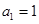 ,对于任意的
,对于任意的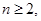 恒有
恒有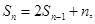
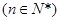
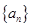 的通项公式
的通项公式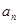
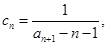 证明:
证明:
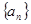 中,
中,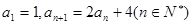 ,则通项公式
,则通项公式 =
=  ,,则
,,则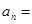 .
.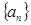 满足
满足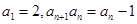 ,则
,则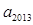 的值为
的值为