题目内容
15.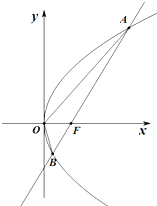 已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.
已知抛物线C:y2=2px(p>0)的焦点为F(1,0),过F且斜率为1的直线l交抛物线C于A(x1,y1),B(x2,y2)两点.(Ⅰ)求抛物线C的标准方程;
(Ⅱ)求△OAB的面积.
分析 (Ⅰ)由抛物线的焦点坐标,可得p=2,进而得到抛物线方程;
(Ⅱ)求出直线方程,代入抛物线方程,运用韦达定理和弦长公式,再由点到直线的距离公式,运用三角形的面积公式计算即可得到所求值.
解答 解:(Ⅰ)由抛物线C:y2=2px(p>0)的焦点为F(1,0),
即有$\frac{p}{2}$=1,解得p=2.
即有抛物线方程为y2=4x;
(Ⅱ)直线方程为y=x-1,
联立抛物线得x2-6x+1=0,
故x1+x2=6,x1x2=1,
即有|AB|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{2}$•$\sqrt{36-4}$=8.
又原点到直线距离为d=$\frac{|-1|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
故△OAB的面积为$\frac{1}{2}$•$\frac{\sqrt{2}}{2}$•8=2$\sqrt{2}$.
点评 本题考查抛物线的方程和性质,考查直线和抛物线方程联立,运用韦达定理和弦长公式,考查运算能力,属于中档题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
3.从甲地到乙地,每天有直达汽车4班,从甲地到丙地,每天有5个班车,从丙地到乙地,每天有3个班车,则从甲地到乙地不同的乘车方法有( )
| A. | 12种 | B. | 19种 | C. | 32种 | D. | 60种 |
7.$sin(-\frac{43π}{6})$的值为( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
5.过曲线y=xex上横坐标为1的点的切线方程为( )
| A. | 2ex-y-e=0 | B. | ex-y=0 | C. | x-y+1=0 | D. | x-y-1=0 |
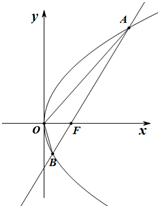 设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4.
设抛物线C:y2=2px(p>0)的焦点为F,过F且斜率为k的直线l交抛物线C于A(x1,y1),B(x2,y2)两点,且y1y2=-4.