Question

【题目】已知四棱锥的正视图是一个底边长为4腰长为3的等腰三角形，图1、图2分别是四棱锥的侧视图和俯视图.

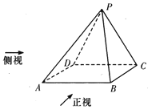
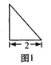
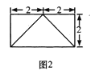
（1）求证：；

（2）求四棱锥的体积及侧面积.

Answer 1

【答案】（1）证明见解析；（2）体积，侧面积

【解析】

（1）取的中点，连接，则平面，则，再有，利用线面垂直的判定定理证明.

（2）在等腰三角形中，，在中，，即为高，再求得底面的面积，利用锥体体积公式求解.为等腰三角形， 分别为底边上的高，为直角三角形，分别求得其面积即可.

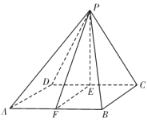
（1）如图所示：

取的中点，连接，则平面，

由

所以平面

又平面，

所以.

（2）依题意，在等腰三角形中，，

在中，，

∴四棱锥的体积为.

过作，垂足为，连接，

∵平面，平面，∴.

∵平面，平面，，

∴平面.∵平面，∴.

依题意得.

在中，，

∴的面积为，

的面积分别为3，3，，

所以侧面积的大小为.