题目内容
16. 如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE
如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE(Ⅰ)求证:AE⊥BE
(Ⅱ)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.
分析 (Ⅰ)推导出BC⊥平面ABE,从而AE⊥BC,由BF⊥平面ACE,得AE⊥BF,从而AE⊥平面BCE,由此能证明AE⊥BE.
(Ⅱ)在三角形ABE中过M点作MG∥AE交BE于G点,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,由比例关系得CN=$\frac{1}{3}$CE,推导出平面MGN∥平面ADE,由此能求出N点为线段CE上靠近C点的一个三等分点.
解答 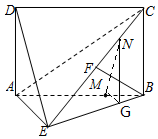 证明:(Ⅰ)∵AD⊥平面ABE,AD∥BC
证明:(Ⅰ)∵AD⊥平面ABE,AD∥BC
∴BC⊥平面ABE,∵AE?平面ABE,∴AE⊥BC,
又∵BF⊥平面ACE,AE?平面ACE,∴AE⊥BF,
∵BC∩BF=B,∴AE⊥平面BCE,
又BE?平面BCE,∴AE⊥BE.(6分)
解:(Ⅱ)在三角形ABE中过M点作MG∥AE交BE于G点,
在三角形BEC中过G点作GN∥BC交EC于N点,连MN,
则由比例关系得CN=$\frac{1}{3}$CE,
∵MG∥AE MG?平面ADE,AE?平面ADE,∴MG∥平面ADE,
同理,GN∥平面ADE,∴平面MGN∥平面ADE,
又MN?平面MGN,∴MN∥平面ADE,
∴N点为线段CE上靠近C点的一个三等分点.(12分)
点评 本题考查线线垂直的证明,考查满足线面平行的点的位置的确定,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、空间想象能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.在这四个函数:①y=sin|x|、②y=|sinx|、③y=sin(2x+$\frac{2π}{3}$)、④y=tan(2x+$\frac{2π}{3}$)中,最小正周期为 π 的函数有( )
| A. | ①②③④ | B. | ①②③ | C. | ②③④ | D. | ②③ |
5.有7个灯泡排成一排,现要求至少点亮其中的3个灯泡,且相邻的灯泡不能同时点亮,则不同的点亮方法有( )
| A. | 11种 | B. | 21种 | C. | 120种 | D. | 126种 |
6.在△ABC中,A,B,C所对的边分别为a,b,c,若1+$\frac{tanA}{tanB}$+$\frac{2c}{b}$=0,则A=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,且|F1F2|=4$\sqrt{3}$,M($\sqrt{3}$,-$\frac{\sqrt{13}}{2}$)是椭圆上一点.