题目内容
5.过抛物线y2=8x的焦点F的直线交抛物线A(x1,y1),B(x2,y2)两点,若x1+x2=5,则|AB|=9.分析 法1:容易求出抛物线的焦点F的坐标为(2,0),而由题意可看出直线存在斜率且不为0,可设直线的斜率为k,写出方程为y=k(x-2),带入抛物线方程整理便可得到k2x2-(4k2+8)+4k2=0,由韦达定理即可求出x1+x2和x1x2,根据x1+x2=5即可求出k2的值,从而根据弦长公式即可求出|AB|的值.法2:根据抛物线方程知,p=4,根据抛物线的定义可得答案.
解答 解:法1:抛物线y2=8x的焦点F(2,0),由题意知,过F的直线存在斜率且不为0,设斜率为k,则直线方程为:y=k(x-2);
带入抛物线方程并整理得:k2x2-(4k2+8)x+4k2=0;
∴${x}_{1}+{x}_{2}=\frac{4{k}^{2}+8}{{k}^{2}}=5$,x1x2=4;
∴k2=8;
∴$|AB|=\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{9}•\sqrt{25-16}=9$.
法2:根据抛物线方程知,p=4;
∴根据抛物线的定义得|AB|=x1+x2+p=5+4=9.
故答案为:9.
点评 考查抛物线的标准方程,抛物线的焦点,以及直线的点斜式方程,韦达定理,弦长公式,注意要说明k存在且不为0.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
20.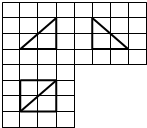 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
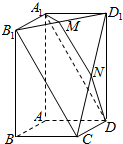 如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.
如图所示,多面体A1B1D1DCBA是长方体A1B1C1D-ABCD被平面B1CD1截去一个三棱锥后所得的几何体,M为B1D1的中点,过A1、D、M的平面交CD1于点N.