题目内容
3.已知正项数列{an},其前n项和为Sn,且an=2$\sqrt{{S}_{n}}$-1.(1)求数列{an}的通项公式;
(2)bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$,求数列{bn}的前n项和.
分析 (1)由题意可得4Sn=(an+1)2,当n≥2时,Sn-Sn-1=an,4Sn=(an+1)2,①,n换为n-1可得4Sn-1=(an-1+1)2,②作差,化简整理可得an-an-1=2,{an}是等差数列,公差是2,求出a1,a2,可得所求通项公式;
(2)求得bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),运用数列的求和方法:裂项相消求和,化简整理即可得到所求和.
解答 解:(1)由an=2$\sqrt{{S}_{n}}$-1,可得:
4Sn=(an+1)2,①
当n≥2时,Sn-Sn-1=an,
n换为n-1可得4Sn-1=(an-1+1)2,②
①-②可得4an=(an+1)2-(an-1+1)2,
化为(an+an-1)(an-an-1-2)=0,
由题意得到an-an-1=2,
∴{an}是等差数列,公差是2,
2$\sqrt{{a}_{1}}$=a1+1,求得a1=1,
故数列{an}的通项公式an=2n-1;
(2)bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
可得数列{bn}的前n项和为$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
点评 本题考查数列的通项公式的求法,注意运用数列的递推式,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案| A. | c>a>b | B. | c>b>a | C. | a>c>b | D. | a>b>c |
| A. | {-2}∪[2,+∞) | B. | (-∞,-2]∪[2,+∞) | C. | [2,+∞) | D. | {0}∪[2,+∞) |
| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
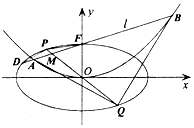 在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.
在平面直角坐标系xOy中,抛物线E:x2=4y的焦点F是椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个顶点.过点F且斜率为k(k≠0)的直线l交椭圆C于另一点D,交抛物线E于A、B两点,线段DF的中点为M,直线OM交椭圆C于P、Q两点,记直线OM的斜率为k',满足$k•k'=-\frac{1}{4}$.