题目内容
5．函数f（x）=（16x-16-x）log2|x|的图象大致为（ ）| A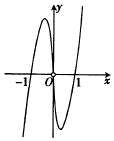． |  | B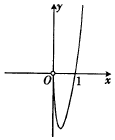． |  | C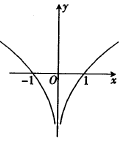． |  | D． |  |
分析 分析函数的奇偶性和当x→0时的极限值，利用排除法，可得函数f（x）的大致图象．
解答 解：∵函数f（x）=（16x-16-x）log2|x|，
∴函数f（-x）=（16-x-16x）log2|-x|=-[（16x-16-x）log2|x|]，
即f（-x）=-f（x），
故函数为奇函数，图象关于原点对称，故排除B，C
当x→0时，$\lim_{x→0}f（x）=0$，故排除D，
故选：A
点评 本题考查的知识点是函数的图象，函数的奇偶性，极限的运算，难度中档．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．圆锥的母线长为L，过顶点的最大截面的面积为$\frac{1}{2}{L}^{2}$，则圆锥底面半径与母线长的比$\frac{r}{L}$的取值范围是（ ）
| A． | 0$＜\frac{r}{L}＜\frac{1}{2}$ | B． | $\frac{1}{2}≤\frac{r}{L}＜1$ | C． | 0$＜\frac{r}{L}＜\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{2}}{2}≤\frac{r}{L}＜1$ |
20．集合M={x|x2＜2x}，N={x|log2（x-1）≤0}，则M∩N=（ ）
| A． | （1，2） | B． | （1，2] | C． | [1，2） | D． | （0，2） |
10．已知函数f（x）=ax3-bx-4，其中a，b为常数．若f（-2）=2，则f（2）的值为（ ）
| A． | -2 | B． | -4 | C． | -6 | D． | -10 |
17．已知双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率等于$\frac{{\sqrt{5}}}{2}$，且点$（{\sqrt{5}，\frac{1}{2}}）$在双曲线C上，则双曲线C的方程为（ ）
| A． | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B． | ${y^2}-\frac{x^2}{4}=1$ | C． | $\frac{y^2}{4}-{x^2}=1$ | D． | $\frac{x^2}{4}-{y^2}=1$ |
14．若将函数$y=sin（{2x+\frac{π}{3}}）$的图象向右平移m（m＞0）个单位长度，所得函数图象关于y轴对称，则m的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{3}$ | C． | $\frac{5π}{12}$ | D． | $\frac{7π}{12}$ |