题目内容
19.已知正数x,y满足x+y=1,则$\frac{4}{x+2}$$+\frac{1}{y+1}$的最小值为$\frac{9}{4}$.分析 由条件可得(x+2)+(y+1)=4,则$\frac{4}{x+2}$$+\frac{1}{y+1}$=$\frac{1}{4}$[(x+2)+(y+1)]($\frac{4}{x+2}$$+\frac{1}{y+1}$),展开后,运用基本不等式即可得到所求最小值,注意等号成立的条件.
解答 解:正数x,y满足x+y=1,
即有(x+2)+(y+1)=4,
则$\frac{4}{x+2}$$+\frac{1}{y+1}$=$\frac{1}{4}$[(x+2)+(y+1)]($\frac{4}{x+2}$$+\frac{1}{y+1}$)
=$\frac{1}{4}$[5+$\frac{x+2}{y+1}$+$\frac{4(y+1)}{x+2}$]
≥$\frac{1}{4}$[5+2$\sqrt{\frac{x+2}{y+1}•\frac{4(y+1)}{x+2}}$]=$\frac{1}{4}$×(5+4)=$\frac{9}{4}$,
当且仅当x=2y=$\frac{2}{3}$时,取得最小值$\frac{9}{4}$.
故答案为:$\frac{9}{4}$.
点评 本题考查了“乘1法”和基本不等式的性质,考查了变形的能力,考查了计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 24 | B. | 48 | C. | 54 | D. | 72 |
11.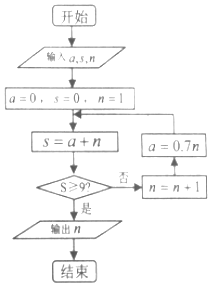 我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
 我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道问题:“今有垣高九尺,瓜生其上,蔓日长七寸;瓠生其下,蔓日长一尺,问几何日相逢?”现用程序框图描述,如图所示,则输出的结果n=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
7.E为正四面体D-ABC棱AD的中点,平面α过点A,且α∥平面ECB,α∩平面ABC=m,α∩平面ACD=n,则m、n所成角的余弦值为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{3}$ |
8.已知集合A={x|x2+x-6<0},B={x|3x>1},则A∩(∁RB)=( )
| A. | (-3,1] | B. | (1,2) | C. | (-3,0] | D. | [1,2) |
9.设集合A={x|x2<2x},B={x|x-1<0},则A∩B=( )
| A. | (-∞,-1) | B. | (-∞,1) | C. | (0,1) | D. | (1,2) |