题目内容
7.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的三个参量a,b,c成等差数列,则该椭圆的离心率( )| A. | $\frac{3}{5}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{3}{5}$或$\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
分析 直接利用椭圆的简单性质以及等差数列关系,求解椭圆的离心率即可.
解答 解:椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的三个参量a,b,c成等差数列,
可得2b=a+c,即$b=\frac{a+c}{2}$,
可得a2-c2=$(\frac{a+c}{2})^{2}$,
可得:3a2-5c2-2ac=0,
可得5e2+2e-3=0,
解得e=$\frac{3}{5}$.
故选:A.
点评 本题考查椭圆的简单性质,等差数列的应用,考查计算能力.

练习册系列答案
相关题目
17.已知tan(α+β)=$\frac{3}{4}$,tan(β-$\frac{π}{4}$)=$\frac{1}{4}$,那么tan(α+$\frac{π}{4}$)=( )
| A. | $\frac{16}{19}$ | B. | $\frac{16}{13}$ | C. | $\frac{13}{16}$ | D. | $\frac{8}{19}$ |
18.已知点A(1,2),B(4,-2),则线段AB的长度为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.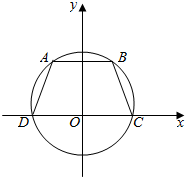 如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
 如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )
如图,已知等腰梯形ABCD的底边长分别为2和14,腰长为10,则这个等腰梯形的外接圆E的方程为( )| A. | x2+(y-2)2=53 | B. | x2+(y-2)2=64 | C. | x2+(y-1)2=50 | D. | x2+(x-1)2=64 |
16.已知x、y∈R,则“x≠3或x≠5”是x+y≠8的( )条件.
| A. | 充分不必要 | B. | 充要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |