题目内容
已知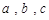 分别是
分别是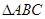 的三个内角
的三个内角 的对边,
的对边, .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求函数 的值域.
的值域.
(Ⅰ) ;(Ⅱ)函数值域为
;(Ⅱ)函数值域为 .
.
解析试题分析:(Ⅰ)因为 ,像这种,式子中即含有边又含有角,往往是要么都化成角,要么都化成边,本题求角
,像这种,式子中即含有边又含有角,往往是要么都化成角,要么都化成边,本题求角 的大小,应利用正弦定理把边化为角得:
的大小,应利用正弦定理把边化为角得: ,去分母整理得
,去分母整理得 ,从而得
,从而得 ,故得
,故得 ;(Ⅱ)求函数
;(Ⅱ)求函数 的值域,含有
的值域,含有 两个角,因此需消去一个角,转化为一个角的一个三角函数来求,由(Ⅰ)可知
两个角,因此需消去一个角,转化为一个角的一个三角函数来求,由(Ⅰ)可知 ,故
,故 ,从而消去C,得关于B的三角函数,利用三角恒等变化及三角函数的单调性来求值域.
,从而消去C,得关于B的三角函数,利用三角恒等变化及三角函数的单调性来求值域.
试题解析:(I)由正弦定理,得:
即
故 4分
4分 ,所以
,所以 6分
6分
(II) 8分
8分 10分
10分
所以所求函数值域为 12分
12分
考点:解三角形,三角恒等变化,三角函数的值域.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 中内角
中内角 的对边分别为
的对边分别为 ,已知
,已知 ,
, .
. 的值;(2)若
的值;(2)若 为
为 中点,且
中点,且 的面积为
的面积为 ,求
,求 的长度.
的长度.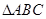 中,角
中,角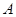 ,
,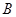 ,
,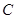 对应的边分别是
对应的边分别是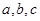 ,已知
,已知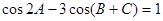 .
.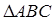 的面积
的面积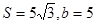 ,求
,求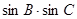 的值.
的值. 中,内角
中,内角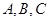 的对边分别为
的对边分别为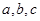 . 已知
. 已知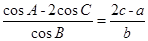 .
.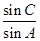 的值; (2) 若
的值; (2) 若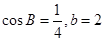 ,求
,求 中,
中, ,
,  的大小;
的大小; 时,求
时,求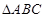 的角
的角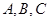 的对边分别为
的对边分别为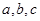 ,已知
,已知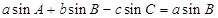 .
.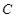 ;
; ,
,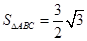 ,求
,求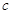 的值.
的值.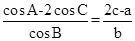 .
.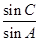 的值;
的值; ,
,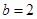 ,求
,求 的面积.
的面积. ,
,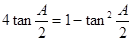 .
.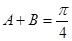 ;
;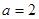 ,求c和ΔABC的面积.
,求c和ΔABC的面积. .
. 的单调递增区间;
的单调递增区间;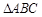 中,三内角
中,三内角 的对边分别为
的对边分别为 ,已知
,已知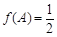 ,
,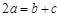 ,
, .求
.求 的值.
的值.