题目内容
1.已知实数x,y满足$\left\{\begin{array}{l}y≥x+2\\ x+y≤6\\ x≥1\end{array}$,其中,则实数$\frac{y}{x+1}$的最小值为$\frac{4}{3}$.分析 由约束条件作出可行域,再由$\frac{y}{x+1}$的几何意义,即可行域内的动点与定点P(-1,0)连线的斜率求解.
解答 解:由约束条件$\left\{\begin{array}{l}y≥x+2\\ x+y≤6\\ x≥1\end{array}$作出可行域如图,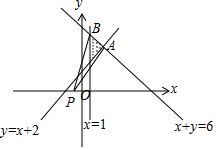
联立$\left\{\begin{array}{l}{y=x+2}\\{x+y=6}\end{array}\right.$,解得A(2,4),
联立$\left\{\begin{array}{l}{x=1}\\{x+y=6}\end{array}\right.$,解得B(1,5),
$\frac{y}{x+1}$的几何意义为可行域内的动点与定点P(-1,0)连线的斜率,
由图可知,$\frac{y}{x+1}$的最小值为$\frac{4-0}{2-(-1)}=\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,是中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
9.已知α为第二象限的角,sinα=$\frac{1}{2}$,β为第一象限的角,cosβ=$\frac{3}{5}$. 则tan(2α-β)的值为( )
| A. | $\frac{{48+25\sqrt{3}}}{39}$ | B. | $\frac{{48-25\sqrt{3}}}{39}$ | C. | $-\frac{{48+25\sqrt{3}}}{39}$ | D. | $-\frac{{48-25\sqrt{3}}}{39}$ |
16.若X~N(-1,62),且P(-3≤X≤-1)=0.4,则P(X≥1)等于( )
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
6.已知函数f(x)=$\left\{\begin{array}{l}a{x^2}+3,x≥0\\({a+2}){e^{ax}},x<0\end{array}$为R上的单调函数,则实数a的取值范围是( )
| A. | [-1,0) | B. | (0,1] | C. | (-2,0) | D. | (-∞,-2) |
10.命题“$?{x_0}∈R,x_0^3-x_0^2+1>0$”的否定是( )
| A. | ?x∈R,x3-x2+1≤0 | B. | $?{x_0}∈R,x_0^3-x_0^2+1<0$ | ||
| C. | $?{x_0}∈R,x_0^3-x_0^2+1≤0$ | D. | $?x∈R,x_0^3-x_0^2+1>0$ |