题目内容
已知直线y=kx与圆x2+y2=3相交于M，N两点，则|MN|等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
考点：直线与圆相交的性质
专题：直线与圆
分析：直线y=kx经过圆x2+y2=3的圆心（0，0），由此能求出|MN|．
解答：
解：∵直线y=kx经过圆x2+y2=3的圆心（0，0），
∴|MN|是直径，
∴|MN|=2
．
故选：D．
∴|MN|是直径，
∴|MN|=2
| 3 |
故选：D．
点评：本题考查弦长的求法，是基础题，解题的关键是判断出直线经过圆心．
练习册系列答案
相关题目
下列是二元一次不等式2x-y+6≤0的解所表示的平面区域的是（ ）
A、 |
B、 |
C、 |
D、 |
若a=2
，b=3
，c=log32
，则（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |
若等差数列{an}的前n项和为Sn，且Sn的最大值仅为S7，则下列说法错误的是（ ）
| A、等差数列{an}中，公差d＜0 |
| B、等差数列{an}中，首项a1＞0 |
| C、等差数列{an}中，an的最大值为a7 |
| D、等差数列{an}中，当正整数n≥8时，an＜0 |
已知，如图，在梯形ABCD中，AD∥BC，AD=3，BC=7，点M，N分别是对角线BD，AC的中点，则MN=（ ）| A、2 | ||
| B、5 | ||
C、
| ||
D、
|
函数f（x）=x•e-x的一个单调递增区间是（ ）
| A、[∞，1] |
| B、[-∞，-1] |
| C、[1，+∞] |
| D、[-1，+∞] |
用反证法证明某命题时，对结论：“自然数a，b，c都是偶数”，正确的反设为（ ）
| A、a，b，c中至少有一个是奇数 |
| B、a，b，c中至多有一个是奇数 |
| C、a，b，c都是奇数 |
| D、a，b，c中恰有一个是奇数 |
已知数列的前四项为1×2，2×3，3×4，4×5，则下列可以做为该数列通项的是（ ）
| A、2n |
| B、n+1 |
| C、n2+n |
| D、n2-n |
| E、n2+n |
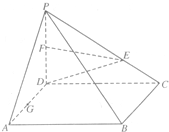如图，ABCD是正方形，PD⊥底面ABCD，点E在PC上，F，G分别是PD和AD的中点．