题目内容

设△ABC的内角A，B，C所对应的边分别为a，b，c，且a+c=7．a＞c，b=2，cosB=
7
8
，求a，c的值．
考点：正弦定理
专题：解三角形
分析：直接利用余弦定理故选a、c关系式．然后求解即可．
解答： 解：由余弦定理可得：b2=a2+c2-2ac×
7
8
=4，即4a2+4c2-7ac-16=0，又a+c=7，
解得：c=3，a=4或c=4，a=3，
∵a＞c，
∴c=3，a=4．
点评：本题考查余弦定理的应用，基本知识的考查．
练习册系列答案
相关题目
当a≥b＞0时，双曲线
x2
a2
-
y2
b2
=1的离心率e的取值范围是（　　）
A、（0，
2
2
]
B、[
2
2
，1）
C、（1，
2
]
D、[
2
，+∞）
已知i为虚数单位，复数z=2i（2-i）的实部为a，虚部为b，则logab等于（　　）
A、0B、1C、2D、3
在数列中，a1=1，数列{an+1-3an}是首项为9，公比为3的等比数列．
（Ⅰ）求a2，a3；
（Ⅱ）求数列{
an
3n
}的前n项和Sn．
在数列{an}和{bn}中，an=an，bn=（a+1）n+b，n=1，2，3，…，其中a≥2且a∈Z，b∈R．
（Ⅰ）若a1=b1，a2＜b2，求数列{bn}的前n项和；
（Ⅱ）证明：当a=2，b=
2
时，数列{bn}中的任意三项都不能构成等比数列；
（Ⅲ）设A={a1，a2，a3，…}，B={b1，b2，b3，…}，设C=A∩B．当b=1时，求出相应的集合C．
已知圆C：x2+y2+2x-3=0，直线l1与圆C相交于不同的A、B两点，点M（0，1）是线段AB的中点．
（1）求直线l1的方程；
（2）是否存在与直线l1平行的直线l2，使得l2与圆C相交于不同的两点E、F（l2不经过圆心C），且△CEF的面积S最大？若存在，求出l2的方程及对应的△CEF的面积S．若不存在，请说明理由．
判定函数f（x）=
x2-2
+
2-x2
的奇偶性．
在平面直角坐标系中，曲线C1的参数方程为
x=acosφ
y=bsinφ
（a＞b＞0，φ为参数），且曲线C1上的点M（2，
3
）对应的参数φ=
π
3
．且以O为极点，X轴的正半轴为极轴建立极坐标系，曲线C2是圆心在极轴上且经过极点的圆，射线θ=
π
4
与曲线C2交于点D（
2
，
π
4
）．
（1）求曲线C1的普通方程，C2的极坐标方程；
（2）若A（ρ1，θ），B（ρ2，θ+
π
2
）是曲线C1上的两点，求
1
ρ12
+
1
ρ22
的值．
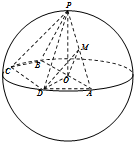如图，平面四边形ABCD的四个顶点都在球O的表面上，AB为球O的直径，P为球面上一点，且PO⊥平面ABCD，NC=CD=DA=2，点M为PA的中点．
（1）证明：平面PBC∥平面ODM；
（2）求平面PBC与平面PAD所成锐二面角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网