题目内容
满足线性约束条件
的目标函数z=x-2y的最小值为( )
|
| A、0 | B、-1 | C、2 | D、-3 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的几何意义,进行求最值即可.
解答:
 解:由z=x-2y得y=
解:由z=x-2y得y=
x-
,
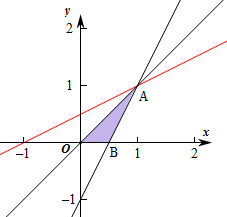
作出不等式组对应的平面区域如图(阴影部分OAB):
平移直线y=
x-
,
由图象可知当直线y=
x-
,过点A时,直线y=
x-
的截距最大,此时z最小,
由
,解得
,即A(1,1).
代入目标函数z=x-2y,
得z=1-2=-1
∴目标函数z=x-2y的最小值是-1.
故选:B.
 解:由z=x-2y得y=
解:由z=x-2y得y=| 1 |
| 2 |
| z |
| 2 |
作出不等式组对应的平面区域如图(阴影部分OAB):
平移直线y=
| 1 |
| 2 |
| z |
| 2 |
由图象可知当直线y=
| 1 |
| 2 |
| z |
| 2 |
| 1 |
| 2 |
| z |
| 2 |
由
|
|
代入目标函数z=x-2y,
得z=1-2=-1
∴目标函数z=x-2y的最小值是-1.
故选:B.
点评:本题主要考查线性规划的基本应用,利用目标函数的几何意义是解决问题的关键,利用数形结合是解决问题的基本方法.

练习册系列答案
相关题目
若集合A={x||x|≤1},B={x|2x>0},A∩B=( )
| A、∅ |
| B、{x|0≤x≤1} |
| C、{x|-1≤x≤1} |
| D、{x|0<x≤1} |
已知直线l:mx-y-m+1=0(m∈R),若存在实数m,使得直线l被曲线C所截得的线段长度为|m|,则称曲线C为l的“优美曲线”.下面给出的曲线:
①y=-|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中是直线l的“优美曲线”的有( )
①y=-|x-1|;
②(x-1)2+(y-1)2=1;
③x2+3y2=4.
其中是直线l的“优美曲线”的有( )
| A、①② | B、③ | C、②③ | D、①②③ |
在△ABC中,A,∠B,∠C所对的边分别为a,b,c,若cos2B+cosB+cos(A-C)=1,则下列说法正确的是( )
| A、a,b,c三边成等比数列 |
| B、a,b,c三边成等差数列 |
| C、a,c,b三边成等比数列 |
| D、a,c,b三边成等差数列 |
已知数列{an}前n项的和Sn=an2+bn(a≠0)是数列{an}成等差数列的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
曲线C:f(x,y)=0关于直线l:x-y-3=0的对称曲线C′的方程是( )
| A、f(x-3,y)=0 |
| B、f(y+3,x)=0 |
| C、f(y-3,x+3)=0 |
| D、f(y+3,x-3)=0 |
函数y=
sinx-
cosx的最小正周期是( )
| 1 |
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
| C、π | ||
| D、2π |
已知实数x,y满足
,则目标函数z=x+y的最大值为( )
|
| A、2 | B、0 | C、9 | D、8 |