题目内容
平移f (x)=sin(ωx+?)(ω>0,- <?<
<?< ),给出下列4个论断:(1)图象关于x=
),给出下列4个论断:(1)图象关于x= 对称(2)图象关于点(
对称(2)图象关于点( ,0)对称 (3)最小正周期是π (4)在[-
,0)对称 (3)最小正周期是π (4)在[- ,0]上是增函数以其中两个论断作为条件,余下论断为结论,写出你认为正确的两个命题:(1)________.(2)________.
,0]上是增函数以其中两个论断作为条件,余下论断为结论,写出你认为正确的两个命题:(1)________.(2)________.
解:(1):①②?③④.
由①得ω× +∅=kπ+
+∅=kπ+ ,k∈z. 由②得ω
,k∈z. 由②得ω  +∅=kπ,k∈z.
+∅=kπ,k∈z.
又∵ω>0,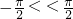 ,故有ω=2,∅=
,故有ω=2,∅= .
.
∴ ,其周期为π.
,其周期为π.
令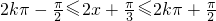 ,可得
,可得 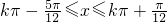 .
.
故函数f(x)的增区间为[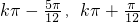 ],k∈z.
],k∈z.
∵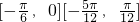 ,
,
∴f(x)在区间[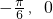 ]上是增函数,
]上是增函数,
故可得 ①②?③④.
(2):还可①③?②④.
由③它的周期为π,可得ω=2,故 f(x)=sin(2x+∅).
由①得 2× +∅=kπ+
+∅=kπ+ ,k∈z.再由
,k∈z.再由 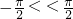 可得φ=
可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ).
).
显然它的图象关于点( ,0)对称,由(1)可得 f(x)在区间[
,0)对称,由(1)可得 f(x)在区间[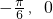 ]上是增函数.
]上是增函数.
故可得 ①③?②④.
故答案为 (1):①②?③④; (2):①③?②④.
分析:(1)由①得ω× +∅=kπ+
+∅=kπ+ ; 再由②得ω
; 再由②得ω  +∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④.
+∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④.
(2)由③可得ω=2,故 f(x)=sin(2x+∅),再由①得 2× +∅=kπ+
+∅=kπ+ ,k∈z,结合∅的范围可得φ=
,k∈z,结合∅的范围可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ),由此推出②④成立.
),由此推出②④成立.
点评:本题主要考查三角函数的周期性,单调性,对称性,以及学生构造命题拓展问题的能力,属中档题.
由①得ω×
 +∅=kπ+
+∅=kπ+ ,k∈z. 由②得ω
,k∈z. 由②得ω  +∅=kπ,k∈z.
+∅=kπ,k∈z.又∵ω>0,
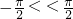 ,故有ω=2,∅=
,故有ω=2,∅= .
.∴
 ,其周期为π.
,其周期为π.令
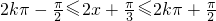 ,可得
,可得 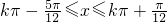 .
.故函数f(x)的增区间为[
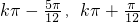 ],k∈z.
],k∈z.∵
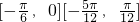 ,
,∴f(x)在区间[
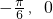 ]上是增函数,
]上是增函数,故可得 ①②?③④.
(2):还可①③?②④.
由③它的周期为π,可得ω=2,故 f(x)=sin(2x+∅).
由①得 2×
 +∅=kπ+
+∅=kπ+ ,k∈z.再由
,k∈z.再由 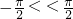 可得φ=
可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ).
).显然它的图象关于点(
 ,0)对称,由(1)可得 f(x)在区间[
,0)对称,由(1)可得 f(x)在区间[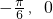 ]上是增函数.
]上是增函数.故可得 ①③?②④.
故答案为 (1):①②?③④; (2):①③?②④.
分析:(1)由①得ω×
 +∅=kπ+
+∅=kπ+ ; 再由②得ω
; 再由②得ω  +∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④.
+∅=kπ,k∈z,以及ω、∅的范围,求得ω、∅的值,从而得函数解析式,从而求出周期和单调增区间,可得③④正确,故得①②?③④.(2)由③可得ω=2,故 f(x)=sin(2x+∅),再由①得 2×
 +∅=kπ+
+∅=kπ+ ,k∈z,结合∅的范围可得φ=
,k∈z,结合∅的范围可得φ= ,故函数f(x)=sin(2x+
,故函数f(x)=sin(2x+ ),由此推出②④成立.
),由此推出②④成立.点评:本题主要考查三角函数的周期性,单调性,对称性,以及学生构造命题拓展问题的能力,属中档题.

练习册系列答案
相关题目
 已知函数f(x)=sin(ωx+
已知函数f(x)=sin(ωx+