Question

已知函数f（x）=sin（ωx+

π

3

）（x∈R，ω＞0）的图象如图，P是图象的最高点，Q是图象的最低点．且|PQ|=

13

．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）将函数y=f（x）图象向右平移1个单位后得到函数y=g（x）的图象，当x∈[0，2]时，求函数h（x）=f（x）•g（x）的最大值．

Answer 1

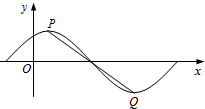
分析：（Ⅰ）由余弦定理得cos∠POQ 的值，可得sin∠POQ，求出P的坐标可得A的值，再由函数的周期求出ω的值，再把点P的坐标代入函数解析式求出φ，即可求得 y=f（x） 的解析式．
（Ⅱ）求出g（x） 的解析式，化简h（x）=f（x）g（x）的解析式，再根据x的范围求出h（x） 的值域，从而求得h（x） 的最大值．

解答：解：（Ⅰ）过P作x轴的垂线PM过Q作y轴的垂线QM，则由已知得|PM|=2，|PQ|=

13

，由勾股定理得|QM求=3，∴T=6，
又T=

2π

ω

，∴ω=

π

3

，
∴函数y=f（x）的解析式：f（x）=sin（

π

3

x+

π

3

）；
（Ⅱ）将函数y=f（x）图象向右平移1个单位后得到函数y=g（x）的图象，
∴g（x）=sin

π

3

x．
函数h（x）=f（x）•g（x）=sin（

π

3

x+

π

3

） sin

π

3

x=

1

2

sin²

π

3

x+

3

2

sin

π

3

xcos

π

3

x
=

1

4

（1-cos

2π

3

x）+

3

4

sin

2π

3

x=

1

2

sin（

2π

3

x-

π

6

）+

1

4

．…（10分）
当x∈[0，2]时，

2π

3

x-

π

6

∈[-

π

6

，

7π

6

]，
∴当

2π

3

x-

π

6

=

π

2

，
即 x=1时，h_max（x）=

3

4

．

点评：本题主要考查函数y=Asin（ωx+∅）的部分图象求解析式，三角函数的最值的求法与应用，考查计算能力属于中档题．