题目内容

16．已知α为第四象限角，sinα+cosα=$\frac{1}{5}$，则tanα的值为-$\frac{3}{4}$．

分析 利用同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得cosα，sinα的值，可得tanα的值．

解答 解：∵α为第四象限角，sinα+cosα=$\frac{1}{5}$，∴sinα＜0，cosα＞0，
∴1+2sinαcosα=$\frac{1}{25}$，2sinαcosα=-$\frac{24}{25}$，
∴cosα-sinα=$\sqrt{{（cosα-sinα）}^{2}}$=$\sqrt{1-2sinαcosα}$=$\frac{7}{5}$，
解得sinα=-$\frac{3}{5}$，cosα=$\frac{4}{5}$，
则tanα=$\frac{sinα}{cosα}$=-$\frac{3}{4}$，
故答案为：-$\frac{3}{4}$．

点评 本题主要考查同角三角函数的基本关系的应用，以及三角函数在各个象限中的符号，属于基础题．

练习册系列答案
相关题目
6．已知三棱锥P-ABC的四个顶点均在半径为1的球面上，且满足$\overrightarrow{PA}$$•\overrightarrow{PB}$=0，$\overrightarrow{PB}$$•\overrightarrow{PC}$=0，$\overrightarrow{PC}$$•\overrightarrow{PA}$=0，则三棱锥P-ABC的侧面积的最大值为（　　）
A．1B．2C．4D．8
7．已知抛物线G：x2=2py（p＞0），直线y=k（x-1）+2与抛物线G相交A（x1，y1），B（x2，y2）（x1＜x2），过A，B点分别作抛物线G的切线L1，L2，两切线L1，L2相交H（x，y），
（1）若k=1，有 L1⊥L2，求抛物线G的方程；
（2）若p=2，△ABH的面积为S1，直线AB与抛物线G围成封闭图形的面积为S2，证明：$\frac{S_1}{S_2}$为定值．
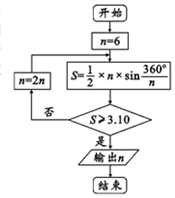4．公元263年左右，我国数学家刘徽发现，当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，由此创立了割圆术，利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的徽率．如图是利用刘徽的割圆术设计的程序框图，则输出的n值为（　　）
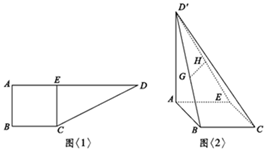参考数据：$\sqrt{3}=1.732$，sin15°≈0.2588，sin7.5°≈0.1305．
A．12B．24C．48D．96
11．如图＜1＞：在直角梯形ABCD中，AD∥BC，∠ABC=90°，AB=BC=2，AD=6，CE⊥AD于E点，把△DEC沿CE折到D′EC的位置，使D′A=2$\sqrt{3}$，如图＜2＞：若G，H分别为D′B，D′E的中点．
（Ⅰ）求证：GH⊥D′A；
（Ⅱ）求三棱锥C-D′BE的体积．
1．若数列{an}是公差为2的等差数列，数列{bn}满足b1=1，b2=2，且anbn+bn=nbn+1．
（Ⅰ）求数列{an}、{bn}的通项公式；
（Ⅱ）设数列{cn}满足cn=$\frac{{a}_{n}+1}{{b}_{n+1}}$，数列{cn}的前n项和为Tn，若不等式（-1）nλ＜Tn+$\frac{n}{{2}^{n-1}}$对一切n∈N*，求实数λ的取值范围．
8．已知数列{an}中，a3=5，a5+a6=20，且2${\;}^{{a}_{n}}$，2${\;}^{{a}_{n+1}}$，2${\;}^{{a}_{n+2}}$成等比数列，数列{bn}满足bn=an-（-1）nn．
（Ⅰ）求数列{bn}的通项公式；
（Ⅱ）设sn是数列{bn}前n项和，求sn．
5．已知$A（3，0），B（0，3），C（cosα，sinα），\overrightarrow{AC}⊥\overrightarrow{BC}$，则sin2α的值为（　　）
A．$\frac{8}{9}$B．$-\frac{8}{9}$C．$\frac{{2\sqrt{2}}}{3}$D．$-\frac{{2\sqrt{2}}}{3}$
6．已知直线l1：y=k（x+1）+2，（k∈R）过定点P．
（1）求定点P的坐标；
（2）若直线l1与直线l2：3x-（k-2）y+5=0平行，求k的值并求此时两直线间的距离．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网