题目内容
已知a为实数，且函数f(x)=(x2-4)(x-a)
(1)求导函数f′(x)；
(2)若f′(-1)=0，求函数f(x)在［-2,2］上的最大值、最小值.
解：(1)f(x)=(x2-4)(x-a)=x3-ax2-4x+4a得f′(x)=3x2-2ax-4.
(2)∵f′(-1)=0,
∴a=
，
∴f(x)=x3-x2-4x+2，
∴f′(x)=3x2-x-4.
令f′(x)=0，
∴3x2-x-4=0，
解得x=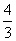
或x=-1.
当x<-1或x>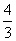时，f′(x)>0，f(x)单调递增；
当-1<x<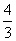时，f′(x)<0，f(x)单调递减.
∵-
<0，
>0,
∴f(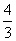)<f(-2)，f(-1)>f(2),
∴函数f(x)在［-2,2］上的最大值、最小值分别为、-.
练习册系列答案
全优点练单元计划系列答案
相关题目
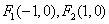,过点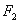
垂直与长轴的直线交
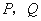两点,且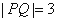
.（Ⅰ）求椭圆的标准方程；（Ⅱ）过
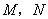,则
的内切圆面积是否存在最大值?若存在,则求出这个最大值及此时的直线
满足
，若
的最大值为
则
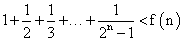(n≥2，n∈N*)的过程，由n=k到n=k+1时，左边增加了( )
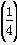x，g(x)＝log
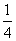x－
a)≤2f(1)，则a的取值范围是( )
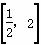D．(0,2]
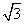，b＝5，求sin Bsin C的值．