题目内容
如图,椭圆 过点P(1,
过点P(1,  ),其左、右焦点分别为F1,F2,离心率e=
),其左、右焦点分别为F1,F2,离心率e=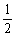 , M, N是直线x=4上的两个动点,且
, M, N是直线x=4上的两个动点,且 ·
· =0.
=0.
(1)求椭圆的方程;
(2)求|MN|的最小值;
(3)以MN为直径的圆C是否过定点?请证明你的结论。

解:(1)∵e= ,且过点P(1,
,且过点P(1, )
)
∴ 解得:a=2,b=
解得:a=2,b=
∴椭圆方程为 =1
=1
(2)设点M(4,y1),N(4,y2),则 =(5,y1),
=(5,y1), =(3,y2),
=(3,y2),
则 =15+y1·y2=0,∴y1·y2=-15
=15+y1·y2=0,∴y1·y2=-15
又∵|MN|=|y2-y1|=|― ―y1|=
―y1|= +|y1|≥2
+|y1|≥2
∴|MN|的最小值为2 。(y1=±
。(y1=± 等号成立)
等号成立)
(3)圆心C的坐标为(4, ),半径r=
),半径r= ,圆C的施方程为:
,圆C的施方程为:
(x-4)2+(y- )2=
)2=
整理得x2+y2―8x―(y1+y2)y+16+y1·y2=0
∵y1·y2=-15 ∴x2+y2―8x―(y1+y2)y+1=0
令y=0,得x2-8x+1=0,∴x=4± ,
,
∴圆C过定点(4,± ,0)
,0)

练习册系列答案
相关题目
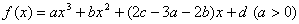 的图像如图所示,且
的图像如图所示,且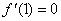 .则
.则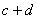 的值是 .
的值是 . 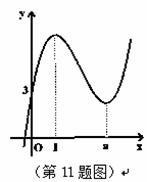
 πa2 D.
πa2 D. πa2
πa2 
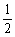 ,
, )的切线的倾斜角是
)的切线的倾斜角是 的图象与函数g(x)=log2x图象交点个数是
的图象与函数g(x)=log2x图象交点个数是 ,
,  满足|
满足| |
| B.
B. C.
C.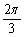 D.
D.