题目内容
已知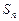 是数列
是数列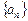 的前n项和,
的前n项和,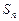 满足关系式
满足关系式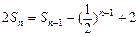 ,
,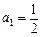
(n≥2,n为正整数).
(1)令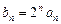 ,证明:数列
,证明:数列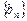 是等差数列;
是等差数列;
(2)求数列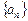 的通项公式;
的通项公式;
(3)对于数列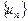 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的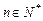 ,恒有
,恒有
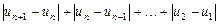 ≤M成立,称数列
≤M成立,称数列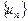 为“差绝对和有界数列”,
为“差绝对和有界数列”,
证明:数列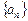 为“差绝对和有界数列”.
为“差绝对和有界数列”.
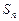 是数列
是数列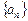 的前n项和,
的前n项和,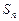 满足关系式
满足关系式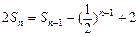 ,
,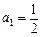
(n≥2,n为正整数).
(1)令
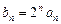 ,证明:数列
,证明:数列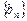 是等差数列;
是等差数列;(2)求数列
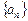 的通项公式;
的通项公式;(3)对于数列
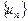 ,若存在常数M>0,对任意的
,若存在常数M>0,对任意的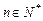 ,恒有
,恒有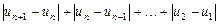 ≤M成立,称数列
≤M成立,称数列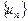 为“差绝对和有界数列”,
为“差绝对和有界数列”,证明:数列
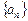 为“差绝对和有界数列”.
为“差绝对和有界数列”.(1) 见解析 (2) (3)见解析
(3)见解析
 (3)见解析
(3)见解析(1)当 时,
时, ,
,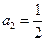

所以 ,
,
即 ,
,
所以
即 ,
, 
又
所以, ,
,
即 为等比数列
为等比数列
(2)


(3)由于
 (求和3分)
(求和3分)
所以 恒成立,即
恒成立,即 为“差绝对和有界数列”。
为“差绝对和有界数列”。
 时,
时, ,
,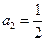

所以
 ,
, 即
 ,
, 所以

即
 ,
, 
又

所以,
 ,
,
即
 为等比数列
为等比数列 (2)



(3)由于

 (求和3分)
(求和3分) 所以
 恒成立,即
恒成立,即 为“差绝对和有界数列”。
为“差绝对和有界数列”。 
练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 平面上有一系列点
平面上有一系列点
 对每个自然数
对每个自然数 ,点
,点 位于函数
位于函数 的图象上.以点
的图象上.以点 与
与 轴都相切,且⊙
轴都相切,且⊙ 又彼此外切.若
又彼此外切.若 ,且
,且
 .
. 是等差数列;
是等差数列; ,
, , 求证:
, 求证:
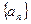 中,
中,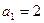 ,
,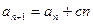 (
(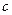 是常数,
是常数,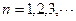 ),且
),且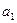 ,
,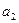 ,
,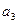 成公比不为
成公比不为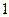 的等比数列.
的等比数列.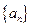 的前n项和为
的前n项和为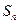 ,已知
,已知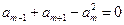 ,
,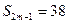 ,则
,则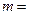
 和
和 都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列
都是等差数列,其中a1=5,b1=10,且a50+b50=20,则数列 的前50项和为( )
的前50项和为( ) 为二次函数,不等式
为二次函数,不等式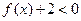 的解集为
的解集为 ,且对任意
,且对任意 ,恒有
,恒有 .
.  满足
满足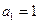 ,
,
 .
.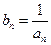 ,求数列
,求数列 的通项公式;
的通项公式; 项和为
项和为 ,求数列
,求数列 的前
的前 .
. 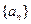 的前
的前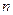 项和
项和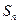 ,且
,且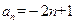 ,则数列
,则数列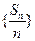 的前11项和为
的前11项和为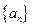 和
和 的前n项和分别为
的前n项和分别为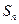 和
和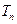 ,若对一切正整数n都有
,若对一切正整数n都有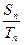 =
=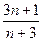 ,则
,则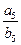 的值为 .
的值为 .