题目内容
3.点P与定点F(2,0)的距离和它到定直线x=$\frac{1}{2}$的距离的比是2:1,求点P的轨迹方程,并说明轨迹是什么图形.分析 设出点P的坐标,直接由P与定点F(2,0)的距离和它到定直线x=$\frac{1}{2}$的距离比是2:1列式整理得方程.
解答 解:设P(x,y),
|PF|=$\sqrt{(x-2)^{2}+{y}^{2}}$,P到定直线x=$\frac{1}{2}$的距离为|x-$\frac{1}{2}$|,
由P与定点F(2,0)的距离和它到定直线x=$\frac{1}{2}$的距离比是2:1=2,得$\frac{\sqrt{(x-2)^{2}+{y}^{2}}}{|x-\frac{1}{2}|}=2$,
整理得:${x}^{2}-\frac{{y}^{2}}{3}=1$.
∴点P的轨迹方程为${x}^{2}-\frac{{y}^{2}}{3}=1$.
是焦点在x轴上的双曲线.
点评 本题考查了与直线有关的动点的轨迹方程,考查了点到直线的距离公式,是中档题.

练习册系列答案
相关题目
11.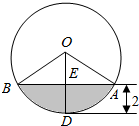 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |
8.将n2个数排成n行n列的一个数阵:
a11 a12 a13…a1n
a21 a22 a23…a2n
a31 a32 a33…a3n
…
an1 an2 an3…ann
已知a11=2,a13=a61+1,该数阵第一列的n个数从上到下构成以m(m>0)为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列,则第7行第5列的数a75=( )
a11 a12 a13…a1n
a21 a22 a23…a2n
a31 a32 a33…a3n
…
an1 an2 an3…ann
已知a11=2,a13=a61+1,该数阵第一列的n个数从上到下构成以m(m>0)为公差的等差数列,每一行的n个数从左到右构成以m为公比的等比数列,则第7行第5列的数a75=( )
| A. | 432 | B. | 540 | C. | 1377 | D. | 1620 |
15.某种饮料每瓶售价2元,销售中还规定5个空瓶子可换取一瓶饮料(含瓶),这种饮料每瓶成本1元,那么该种饮料每瓶利润应是( )
| A. | 1元 | B. | 0.66元 | C. | 0.6元 | D. | 0.55元 |
 借助单位圆求sinx=$\frac{1}{2}$时,x的值?
借助单位圆求sinx=$\frac{1}{2}$时,x的值?