题目内容
11.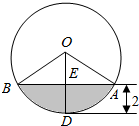 一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )
一个圆柱形的罐子半径是4分米,高是9分米,并在其中注入深度达到h(单位:分米)的水.然后将其平放,截面如图所示,则h(单位:分米)等于( )| A. | 4-$\frac{3\sqrt{3}}{4π}$ | B. | 2-$\frac{3\sqrt{3}}{16π}$ | C. | 3-$\frac{9\sqrt{3}}{4π}$ | D. | 3-$\frac{9\sqrt{3}}{16π}$ |
分析 由已知可得水对应的几何体是一个以截面中阴影部分为底,以9为高的柱体,求出底面面,代入柱体体积公式,可得水的体积,进而得到h值.
解答 解:由已知中罐子半径是4分米,水深2分米,
故截面中阴影部分的面积S=$\frac{1}{3}$π×42-$\frac{\sqrt{3}}{4}$×42=$\frac{16π}{3}$-4$\sqrt{3}$平方分米,
又由圆柱形的罐子的高9分米,
故水的体积V=Sh=48π-36$\sqrt{3}$立方分米,
由圆柱的多方面面积为16π平方分米,
故16π•h=48π-36$\sqrt{3}$,
解得:h=3-$\frac{9\sqrt{3}}{4π}$,
故选:C
点评 本题考查的知识点是柱体的体积公式,扇形面积公式,弓形面积公式,难度中档.

练习册系列答案
相关题目
1.已知椭圆G:$\frac{{x}^{2}}{4}$+y2=1,过点(0,2)作圆x2+y2=1的切线l交椭圆G于A,B两点,
(1)求椭圆G的焦点坐标和离心率.
(2)O为坐标原点,求△OAB的面积.
(1)求椭圆G的焦点坐标和离心率.
(2)O为坐标原点,求△OAB的面积.
6.已知函数f(x)=loga(4-ax)在(-2,2)上是减函数,则a的取值范围是( )
| A. | (0,2) | B. | (1,2) | C. | (1,2] | D. | [2,+∞) |
20.已知三角形的三边长分别为$a,b,\sqrt{{a^2}+{b^2}+\sqrt{3}ab}$,则三角形的最大内角是( )
| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
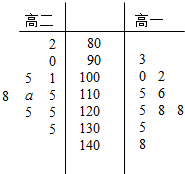 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)