题目内容
16.已知函数f(x)=x3-mx,x∈R,若方程f(x)=2在x∈[-4,4]恰有3个不同的实数解,则实数m的取值范围是$({3,\frac{31}{2}}]$.分析 函数f(x)=x3-mx,x∈R,若方程f(x)=2在x∈[-4,4]恰有3个不同的实数解,则g(x)=x3-mx-2在x∈[-4,4]恰有3个不同的零点,进而求出函数的两个极值点,根据极大值为正,极小值为负,g(-4)不大于0,g(4)不小于0,可得实数m的取值范围.
解答 解:∵函数f(x)=x3-mx,x∈R,若方程f(x)=2在x∈[-4,4]恰有3个不同的实数解,
∴g(x)=x3-mx-2在x∈[-4,4]恰有3个不同的零点,
g′(x)=3x2-m=0时,x=±$\sqrt{\frac{m}{3}}$,
故m>0,且$\sqrt{\frac{m}{3}}$<4,即0<m<48,
且$\left\{\begin{array}{l}g(-4)≤0\\ g(-\frac{m}{3})>0\\ g(\frac{m}{3})<0\\ g(4)≥0\end{array}\right.$,即$\left\{\begin{array}{l}-66+4m≤0\\ \frac{2m}{9}\sqrt{3m}-2>0\\-\frac{2m}{9}\sqrt{3m}-2<0\\ 62-4m≥0\end{array}\right.$,
解得:m∈$({3,\frac{31}{2}}]$,
故答案为:$({3,\frac{31}{2}}]$.
点评 本题考查的知识点是根的存在性及根的个数判断,熟练掌握方程根与对应函数零点之间的关系是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
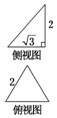 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为2的正三角形,侧视图是有一条直角边为2的直角三角形,则该三棱锥的正视图可能为( )