题目内容
3.从个位数与十位数之和为奇数的两位数中任取一个,其中个位数为0的概率是$\frac{1}{9}$.分析 先求个位数与十位数之和为奇数的两位数的个数n,然后再求个位数与十位数之和为奇数的两位数的个数,由古典概率的求解公式可求.
解答 解:个位数与十位数之和为奇数的两位数中,其个位数与十位数有一个为奇数,一个为偶数,共有C51C51+C51C41=45
记:“个位数与十位数之和为奇数的两位数中,其个位数为0”为事件A,则A包含的结果:10,30,50,70,90共5个
由古典概率的求解公式可得,P(A)=$\frac{5}{45}$=$\frac{1}{9}$.
故答案为:$\frac{1}{9}$.
点评 本题主要考查了古典概率的求解公式的应用,解题的关键是灵活利用简单的排列、组合的知识求解基本事件的个数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.动直线x=m(m>0)与函数f(x)=2x+$\frac{1}{x}$,g(x)=x-$\frac{1}{x}$-lnx分别交于点A,B,则|AB|的最小值为( )
| A. | 3+ln2 | B. | 2 | C. | $\frac{7}{2}$-ln2 | D. | 3 |
11.已知双曲线C:$\frac{{x}^{2}}{m+3}$-$\frac{{y}^{2}}{m}$=1(m>0)的渐近线方程为y=±$\frac{1}{2}$x,则双曲线C的焦距为( )
| A. | 1 | B. | 2$\sqrt{5}$ | C. | 3 | D. | 6 |
15.(文)设全集U=R,集合A={x|x2+4x<0},集合B={x|x<-2},则图中阴影部分表示的集合为( )
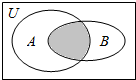

| A. | {x|-4<x<-2} | B. | {x|-4<x<0} | C. | {x|x>0} | D. | {x|x<-2} |
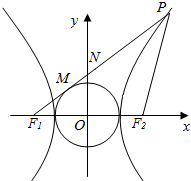 已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.
已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点分别为F1、F2,P为双曲线右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则该双曲线的离心率e是$\frac{5}{3}$.