题目内容
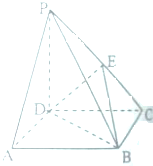 如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.(1)求四棱锥P-ABCD的体积;
(2)若E为PC中点,求证:PA∥平面BDE;
(3)求直线PB与平面ABCD所成角的正切值.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)直接根据已知条件求出锥体的体积.
(2(利用三角形的中位线得到线线平行,进一步转化成线面平行.
(3)直接利用解三角形知识求出线面的夹角的大小.
(2(利用三角形的中位线得到线线平行,进一步转化成线面平行.
(3)直接利用解三角形知识求出线面的夹角的大小.
解答:
解:(1)四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
所以:VP-ABCD=
•S正方形ABCD•PD
=
•a2•a=
证明:(2)在正方形ABCD中,连接AC和BD交与点O,连接OE,
所以:O是AC的中点,
由于E是PC的中点,
所以:OE是△PAC的中位线,
则:OE∥PA
OE?平面BDE
PA?平面BDE,
所以:PA∥平面BDE.
解:(3)PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
则:BD=
a
所以:∠PBD就是PB与平面ABCD所成角.
则:tan∠PBD=
=
所以:直线PB与平面ABCD所成角的正切值为
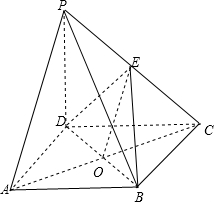
所以:VP-ABCD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| a3 |
| 3 |
证明:(2)在正方形ABCD中,连接AC和BD交与点O,连接OE,
所以:O是AC的中点,
由于E是PC的中点,
所以:OE是△PAC的中位线,
则:OE∥PA
OE?平面BDE
PA?平面BDE,
所以:PA∥平面BDE.
解:(3)PD⊥底面ABCD,底面ABCD是边长为a的正方形,且PD=a.
则:BD=
| 2 |
所以:∠PBD就是PB与平面ABCD所成角.
则:tan∠PBD=
| PD |
| BD |
| ||
| 2 |
所以:直线PB与平面ABCD所成角的正切值为
| ||
| 2 |

点评:本题考查的知识要点:锥体的体积公式的应用,线面平行的判定,线面夹角的应用,属于基础题型.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知函数f(x)=2x2-ax-1,在[-1,2]上单调,则实数a的取值范围是( )
| A、[-4,8] |
| B、(-∞,-4] |
| C、[8,+∞] |
| D、(-∞,-4]∪[8,+∞) |
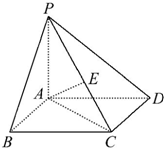 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥AB,PA⊥AC,E是PC的中点,已知AB=2,AD=PA=2,求异面直线BC与AE所成的角的大小.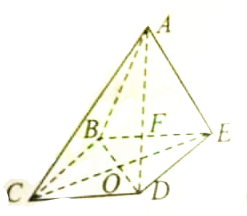 如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;
如图所示,几何体A-BCDE是底面边长为4的菱形,∠CBE=120°,侧面ABE是等边三角形,BD∩CE=O,F是BE上的动点,面ABE⊥面BCDE;