题目内容
如果数列{an}的前n项和为Sn=an2+bn+c(a、b、c为常数),求证:数列{an}是等差数列的充要条件是c=0.
证明:(1)充分性:由c=0
数列{an}是等差数列.
由公式an=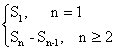
=
∴an=2an+b-a.
又an-an-1=(2an+b-a)-［2a(n-1)+b-a］=2a(常数).
∴{an｝是等差数列.
(2)必要性:由数列{an}是等差数列
c=0.
由公式an=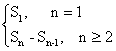
=
∴a1=a+b+c,a2=4a+b-a=3a+b,a3=6a+b-a=5a+b.
∵{an}是等差数列.∴a3-a2=a2-a1.
∴2a=2a-c.∴c=0.
综上,数列{an}是等差数列的充要条件是c=0.
练习册系列答案
三点一测快乐周计划系列答案
相关题目
如果数列{an}的前n项和Sn=2n-1，那么这个数列（ ）
| A、是等差数列但不是等比数列 | B、是等比数列但不是等差数列 | C、既是等差数列又是等比数列 | D、既不是等差数列又不是等比数列 |