题目内容
已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1)求向量b+c的长度的最大值;
(2)设α=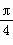 ,且a⊥(b+c),求cos β
,且a⊥(b+c),求cos β 的值.
的值.
 法二 若α=
法二 若α= ,则a=
,则a= .又由b=(cos β,sin β),
.又由b=(cos β,sin β),
c=(-1,0),得a·(b+c)= ·(cos β-1,sin β)=
·(cos β-1,sin β)=
 cos β+
cos β+ sin β-
sin β- .
.
∵a⊥(b+c),∴a·(b+c)=0,即 cos β+sin β=1.
cos β+sin β=1.
∴sin β=1-cos β,平方后化简得cos β(cos β-1)=0,
解得cos β=0或cos β=1.经检验,cos β=0或cos β=1即为所求.

练习册系列答案
相关题目
 ,
, ,
,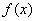 的最大值
的最大值 ;
; 中,
中, ,
, 分别是棱
分别是棱 上的点(点
上的点(点 不同于点
不同于点 ),且
),且 为
为 的中点.
的中点. 平面
平面 ;
; 平面
平面 .
.
 B.-
B.- D.-
D.-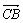 =a,
=a,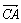 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=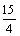 ,|a|=3,|b|1=5,则a与b的夹角为 ( )
,|a|=3,|b|1=5,则a与b的夹角为 ( )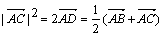
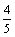 ,且l与D的轨迹相切,求椭圆方程.
,且l与D的轨迹相切,求椭圆方程. 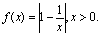
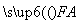 +
+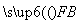 +
+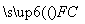 =0,且|
=0,且|