题目内容
已知△ABC中,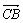 =a,
=a,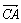 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=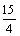 ,|a|=3,|b|1=5,则a与b的夹角为 ( )
,|a|=3,|b|1=5,则a与b的夹角为 ( )
A.30° B.-150°C.150° D.30°或150°
C

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
题目内容
已知△ABC中,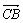 =a,
=a,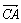 =b,a·b<0,S△ABC=
=b,a·b<0,S△ABC=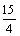 ,|a|=3,|b|1=5,则a与b的夹角为 ( )
,|a|=3,|b|1=5,则a与b的夹角为 ( )
A.30° B.-150°C.150° D.30°或150°
C

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案