题目内容
定义在实数上的函数f(x)=
的最小值是 .
| sinπx | ||
|
考点:三角函数的最值,利用导数求闭区间上函数的最值
专题:计算题,函数的性质及应用,三角函数的图像与性质
分析:根据二次函数的性质可得0<
≤
①,易知-1≤sinπx<0②时,f(x)取得最小值,利用不等式的乘法性质两式相乘可得结果.
| 1 | ||
|
2
| ||
| 3 |
解答:
解:∵
=
≥
,当且仅当x=-
时取等号,
∴0<
≤
①,
又-1≤sinπx≤1,则-1≤sinπx<0时,f(x)取得最小值,
则0<-sinπx≤1②,x=-
时取得等号,
∴不等式①②相乘可得,
≥-
,即函数f(x)的最小值是-
,
故答案为:-
.
| 1+x+x2 |
(x+
|
| ||
| 2 |
| 1 |
| 2 |
∴0<
| 1 | ||
|
2
| ||
| 3 |
又-1≤sinπx≤1,则-1≤sinπx<0时,f(x)取得最小值,
则0<-sinπx≤1②,x=-
| 1 |
| 2 |
∴不等式①②相乘可得,
| sinπx | ||
|
2
| ||
| 3 |
2
| ||
| 3 |
故答案为:-
2
| ||
| 3 |
点评:本题考查函数最值的求解及不等式的性质应用,考查学生综合运用知识分析解决问题的能力.

练习册系列答案
相关题目
甲、乙两人同时从图书馆走向教室,甲一半路程步行,一半路程跑步;乙一半时间步行,一半时间跑步,若两人步行、跑步的速度一样,则先到教室的是( )
| A、甲 | B、乙 |
| C、甲、乙同时到达 | D、无法确定 |
已知实数r是常数,如果M(x0,y0)是圆x2+y2=r2外的一点,那么直线x0x+y0y=r2与圆x2+y2=r2的位置关系是( )
| A、相交 | B、相切 |
| C、相离 | D、都有可能 |
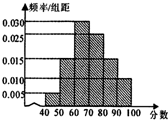 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图,已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为