题目内容
2.已知函数y=f(x)是定义在R上的偶函数,当x≤0时,f(x)=x+2,那么不等式2f(x)-1>0的解集是(-$\frac{3}{2}$,$\frac{3}{2}$).分析 先求出x≤0时不等式的解集,再利用偶函数的性质得出x>0的解集,从而得出不等式的解集.
解答 解:当x≤0时,∵2f(x)-1>0,即2x+4-1>0,
解得x>-$\frac{3}{2}$,∴-$\frac{3}{2}$<x≤0.
∵f(x)是定义在R上的偶函数,
∴当0$<x<\frac{3}{2}$时,2f(x)-1>0仍成立.
∴2f(x)-1>0的解集为(-$\frac{3}{2}$,$\frac{3}{2}$).
故答案为:$(-\frac{3}{2},\frac{3}{2})$.
点评 本题考查了函数奇偶性的性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知函数f(x)=x2-$\frac{a}{x}$(a∈R),则下列结论正确的是( )
| A. | ?a∈R,f(x)是偶函数 | B. | ?a∈R,f(x)是奇函数 | ||
| C. | ?a∈(0,+∞),f(x)在(-∞,0)上是增函数 | D. | ?a∈(0,+∞),f(x)在(0,+∞)上是减函数 |
10.已知i是虚数单位,且$z={(\frac{1-i}{1+i})^{2016}}$+i的共轭复数为$\overline{z}$,则z$•\overline{z}$等于( )
| A. | 2 | B. | 1 | C. | 0 | D. | -l |
7.复数$\frac{1}{1-i}$的虚部是( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | $-\frac{1}{2}i$ |
11.已知向量$\overrightarrow{a}$=(4cosx,$\frac{1}{3}$),$\overrightarrow{b}$=(sin(x+$\frac{π}{6}$),-1),且$\overrightarrow{a}•\overrightarrow{b}$=0,则sin(2x+$\frac{7π}{6}$)=( )
| A. | -$\frac{2\sqrt{2}}{3}$ | B. | -$\frac{1}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
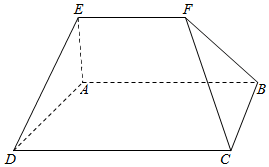 如图,用四种不同颜色的灯泡安装在图中的A,B,C,D,E,F六个点,要求每个点安装一个灯袍,且图中每条线段两个端点的灯泡颜色不同,则不同的安装方法共有多少种?
如图,用四种不同颜色的灯泡安装在图中的A,B,C,D,E,F六个点,要求每个点安装一个灯袍,且图中每条线段两个端点的灯泡颜色不同,则不同的安装方法共有多少种?