Question

19．四棱锥P-ABCD的底面为矩形，且AB=4，BC=3，PD⊥底面ABCD，PD=5，则PB与底面所成角为45°．

Answer 1

分析 画出图形，连接BD，则∠PBD的大小等于直线PB与平面ABCD所成角的大小．

解答 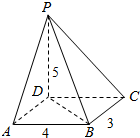解：如图：连接BD，
∵PD⊥ABCD，
∴∠PBD的大小等于直线PB与平面ABCD所成角的大小．
ABCD的底面为矩形，且AB=4，BC=3，可得BD=5，
PD⊥底面ABCD，PD=5，△PDB是等腰直角三角形，∠PBD=45°．
PB与底面所成角为：45°．
故答案为：45°．

点评 本题考查直线与平面所成角的大小，考查空间想象能力以及计算能力．