题目内容
12.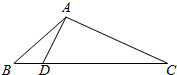 如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.
如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.(I)求AD的长;
(Ⅱ)求cosC.
分析 (Ⅰ)由已知结合三角形中的边角关系求出cos∠BAD的值,在△ABD中,由余弦定理求AD的长;
(Ⅱ)在△ABD中,由正弦定理,求出sin∠ADB,通过三角形是直角三角形,即可求cosC.
解答 解:(Ⅰ)∵∠DAC=90°,
∴sin∠BAC=sin(90°+∠BAD)=cos∠BAD,
∵sin∠BAC=$\frac{2\sqrt{2}}{3}$,
∴cos∠BAD=$\frac{2\sqrt{2}}{3}$,
在△ABD中,由余弦定理可知BD2=AB2+AD2-2AB•ADcos∠BAD,
即AD2-8AD+15=0,
解之得,AD=5或AD=3,
由于AB>AD,
∴AD=3;
(Ⅱ)在△ABD中,由正弦定理可知$\frac{BD}{sin∠BAD}=\frac{AB}{sin∠ADB}$,
又由cos∠BAD=$\frac{2\sqrt{2}}{3}$,
可知sin∠BAD=$\frac{1}{3}$,
∴sin∠ADB=$\frac{ABsin∠BAD}{BD}$=$\frac{\sqrt{6}}{3}$,
∵∠ADB=∠DAC+∠C,∠DAC=90°,
∴cosC=$\frac{\sqrt{6}}{3}$.
点评 本题考查解三角形,余弦定理以及正弦定理的应用,考查计算能力,是中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.已知a<b,则下列各式正确的是( )
| A. | a2<b2 | B. | ac<bc | C. | log2a<log2b | D. | 2a<2b |
 如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.
如图,△PBD是直角三角形,∠PDB=90°,以BA为直径作⊙O,设点C是圆⊙O与直线PD的公共点,若∠ABC=∠DBC.