题目内容
4.设x,y是满足x+y=4的整数,则log2x+log2y的最大值是2.分析 利用对数的运算性质,结合基本不等式求得答案.
解答 解:∵正实数x、y满足x+y=4,
∴log2x+log2y=log2(xy)≤log2$(\frac{x+y}{2})^{2}$=log222=2.
当且仅当x=y=2时取等号.
故答案为:2
点评 本题考查了基本不等式,考查对数的运算法则,属于基础题.

练习册系列答案
相关题目
19.已知定义在[1,16]上的函数f(x)=$\left\{\begin{array}{l}{-4+8|x-\frac{3}{2}|}&{1≤x≤2}\\{\frac{1}{2}f(\frac{x}{2})}&{2<x≤16}\end{array}\right.$,则下列结论中错误的是( )
| A. | f(4)=0 | |
| B. | 函数f(x)的值域为[-4,0] | |
| C. | 将函数f(x)的极值由大到小排列得到数列{an},n∈N*,则{an}的前n项和Sn=-8 | |
| D. | 对任意的x∈[1,16],不等式xf(x)+6≥0 |
2.如图1,已知正方体ABCD-A1B1ClD1的棱长为a,动点M、N、Q分别在线段PM上.当三棱锥Q-BMN的俯视图如图2所示时,三棱锥Q-BMN的正视图面积等于( )


| A. | $\frac{1}{2}$a2 | B. | $\frac{1}{4}$a2 | C. | $\frac{\sqrt{2}{a}^{2}}{4}$ | D. | $\frac{\sqrt{3}{a}^{2}}{4}$ |
 已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.
已知函数f(x)是定义域为R的偶函数,当x≥0时,f(x)=-x2+2x.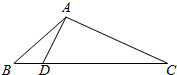 如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.
如图△ABC中,sin∠BAC=$\frac{2\sqrt{2}}{3}$,AB=3$\sqrt{2}$,又己知BC边上有一点D,使∠DAC=90°,BD=$\sqrt{3}$.